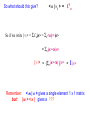* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Slide 1
Quantum field theory wikipedia , lookup
Noether's theorem wikipedia , lookup
Two-body Dirac equations wikipedia , lookup
Electron configuration wikipedia , lookup
Bell's theorem wikipedia , lookup
Molecular Hamiltonian wikipedia , lookup
Hidden variable theory wikipedia , lookup
EPR paradox wikipedia , lookup
Atomic orbital wikipedia , lookup
Path integral formulation wikipedia , lookup
Aharonov–Bohm effect wikipedia , lookup
Renormalization wikipedia , lookup
Schrödinger equation wikipedia , lookup
Quantum electrodynamics wikipedia , lookup
Particle in a box wikipedia , lookup
Quantum state wikipedia , lookup
Bra–ket notation wikipedia , lookup
Atomic theory wikipedia , lookup
Dirac equation wikipedia , lookup
Introduction to gauge theory wikipedia , lookup
History of quantum field theory wikipedia , lookup
Elementary particle wikipedia , lookup
Canonical quantization wikipedia , lookup
Wave function wikipedia , lookup
Scalar field theory wikipedia , lookup
Hydrogen atom wikipedia , lookup
Wave–particle duality wikipedia , lookup
Symmetry in quantum mechanics wikipedia , lookup
Matter wave wikipedia , lookup
Relativistic quantum mechanics wikipedia , lookup
Theoretical and experimental justification for the Schrödinger equation wikipedia , lookup
The tentative schedule of lectures for the semester
with links to posted electronic versions of my notes
can be found at:
http://crop.unl.edu/claes/PHYS926Lectures.html
1936 Millikan’s group shows at earth’s surface cosmic ray showers
are dominated by electrons, gammas, and X-particles
capable of penetrating deep underground
(to lake bottom and deep tunnel experiments)
and yielding isolated single cloud chamber tracks
1937 Street and Stevenson
1938 Anderson and Neddermeyer
determine X-particles
•are charged
•have 206× the electron’s mass
•decay to electrons with
a mean lifetime of 2msec
0.000002 sec
Schrödinger’s Equation
Based on the constant (conserved) value of the Hamiltonian expression
1 2
p V E
2m
total energy sum of KE + PE
with the replacement of variables by “operators”
p
i
E i
t
2
2
V i
t
2m
As enormously powerful and successful as this equation is,
what are its flaws? Its limitations?
We could attempt a RELATIVISTIC FORM of Schrödinger:
What is the relativistic expression for energy?
E 2 p 2c 2 m 2c 4
1
mc
2
2
2
2
c t
2
2
2
relativistic energy-momentum relation
As you’ll appreciate LATER
this simple form (devoid of spin factors)
describes spin-less (scalar) bosons
For m=0 this yields the homogeneous differential equation:
2
1
2
2 2 0
c t
Which you solved in E&M to find that wave equations for
these fields were possible (electromagnetic radiation).
(1935) Hideki Yukawa saw the inhomogeneous
equation as possibly descriptive of a scalar
particle mediating SHORT-RANGE forces
1
mc
2
2
2
2
c t
2
2
2
like the “strong” nuclear force between nucleons
(ineffective much beyond the typical 10-15 meter
extent of a nucleus
2
For a static potential drop 2
t
and assuming a spherically symmetric potential, can cast this equation in the form:
1 2 U
mc
U (r) 2 (r
) 2 U (r)
r r
r
2
2
2
with a solution (you will verify for homework):
g r / R
U (r)
e
4r
where
R=
h
mc
Let’s compare:
g r / R
U (r)
e
4r
to the potential of
electromagnetic fields:
g
U (r)
4r
where
R=
h
mc
with e-r/R=1
its like R
or m = 0!
For a range something like 10-15 m
Yukawa hypothesized the existence
of a new (spinless) boson with
mc2 ~ 100+ MeV.
In 1947 the spin 0 pion was identified with a mass ~140 MeV/c2
1947 Lattes, Muirhead, Occhialini and Powell
observe pion decay
Cecil Powell (1947)
Bristol University
C.F.Powell, P.H. Fowler,
D.H.Perkins
Nature 159, 694 (1947)
Nature 163, 82 (1949)
Quantum Field Theory
Not only is energy & momentum QUANTIZED (energy levels/orbitals)
but like photons are quanta of electromagnetic energy,
all particle states are the physical manifestation of quantum
mechanical wave functions (fields).
Not only does each atomic electron exist trapped
within quantized energy levels or spin states,
but its mass, its physical existence,
is a quantum state of a matter field.
the quanta of the em potential virtual photons
as opposed to observable photons
e
These are not physical photons in orbitals
about the electron. They are continuously
and spontaneously being emitted/reabsorbed.
The Boson Propagator
What is the momentum spectrum of Yukawa’s massive (spin 0) relativistic boson?
Remember it was proposed in analogy to the E&M wave functions of a photon.
What distribution of momentum (available to transfer) does a
quantum wave packet of this potential field carry?
3
1
iqr
q r = qrcos
f (q)
U ( r )e
2
dV
dV = r2 d sin d dr
Integrating the angular part:
3
1 2 2
iqr cos
f (q)
sin d dr
r U ( r ) 0 d 0 e
2
2
1
2
3/ 2
0
e iqr eiqr
iqr
sin qr 2
4 0 U ( r )
r dr
qr
1 2 3/ 2 g
f (q) 2
q m2
1 iqrcos
e
iqr
The more massive the mediating boson,
the smaller this distribution…
Consistently
~600 microns
(0.6 mm)
pdg.lbl.gov/pdgmail
BraKet notation
We generalize the definitions of vectors and inner products ("dot" products) to
extend the formalism to functions (like QM wavefunctions) and differential operators.
v = vx ^x + vy y^ + vz z^
Sn vn ^n
then the inner product is denoted by
v u =
Sn vn un
^=
Remember: n^ m
nm
sometimes represented by row and column matrices:
[vx vy vz ] ux
uy = [ vxux + vyuy + vzuz ]
uz
We most often think of "vectors" in ordinary 3-dim space, but
can immediately and easily generalize to COMPLEX numbers:
v u =
Sn vn* un
[vx* vy* vz* ] ux
uy = [ vx*ux + vy*uy + vz*uz ]
uz
transpose column into row
and take complex conjugate
and by the requirement
<v|u>
=
< v | u >*
we guarantee that the “dot product” is real
Every “vector” is a ket :
including the unit “basis” vectors.
|v1>
We write:
|v> =
|v2>
SnCn | n >
and the scalar product by the symbol
< v |u >
and the orthonormal condition on basis vectors can be stated as
<
Now if we write
| v1 > = SC1n|n>
“we know”:
< v2 | v1 > =
< v2 | | v1 > =
“bra”
and
=
m| n >
mn
| v2 > = SC2n|n> then
SnC2n* C1n
=
Sn,mC2m* C1n<m|n>
SmC2m* <m|SmC1n|n>
because of orthonormality
So what should this give?
C1n
< n | v1 > = ??
So if we write | v > = SCn|n> = Sn<n|v> |n>
= Sn |n><n|v>
| v > = {Sn |n><n| } |v> =
1 |v>
Remember: < m | n > gives a single element 1 x 1 matrix
but: | m > < n | gives a ???
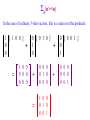
Sn|n><n|
In the case of ordinary 3-dim vectors, this is a sum over the products:
1 [ 1 0 0 ]
0
+
0
=
1 0 0
0 0 0
0 0 0
0 [ 0 1 0 ]
1
+
0
+
0 0 0
0 1 0
0 0 0
=
1 0 0
0 1 0
0 0 1
+
0 [ 0 0 1 ]
0
1
0 0 0
0 0 0
0 0 1
Two important BASIC CONCEPTS
•The “coupling” of a fermion
(fundamental constituent of matter)
to a vector boson
(the carrier or intermediary of interactions)
e
•Recognized symmetries
are intimately related to CONSERVED quantities in nature
which fix the QUANTUM numbers describing quantum states
and help us characterize the basic, fundamental interactions
between particles
Should the selected orientation of the x-axis matter?
As far as the form of the equations of motion?
(all derivable from a Lagrangian)
As far as the predictions those equations make?
Any calculable quantities/outcpome/results?
Should the selected position of the coordinate origin matter?
If it “doesn’t matter” then we have a symmetry:
the x-axis can be rotated through any direction of 3-dimensional space
or
slid around to any arbitrary location
and the basic form of the equations…and, more importantly, all the
predictions of those equations are unaffected.
If a coordinate axis’ orientation or origin’s exact location “doesn’t matter”
then it shouldn’t appear explicitly in the Lagrangian!
EXAMPLE: TRANSLATION
Moving every position (vector) in space by a fixed a
(equivalent to “dropping the origin back” –a)
–a
r' r a
a
dr
r' r
aˆ
dqi q' i qi a
original
description
of position
r
r' new
description
of position
or
dr r (qi dqi ) r ( qi ) dqi aˆ
aˆ
dqi
dqi
dqi
For a system of particles:
T
N
1
2
m
r
2 i
i 1
acted on only by CENTAL FORCES:
d L L
0
dt qk qk
V (r ) V (r)
no forces external
to the system
function of
separation