N - saelim
... A valid codeword of length n can be formed by: A) Adding a digit other than 0 at the end of a valid string of length n – 1 - This can be done in nine ways. Hence, a valid string with n digits can be formed in this manner in 9an 1 ways. B) Adding a digit 0 at the end of an invalid string of length ...
... A valid codeword of length n can be formed by: A) Adding a digit other than 0 at the end of a valid string of length n – 1 - This can be done in nine ways. Hence, a valid string with n digits can be formed in this manner in 9an 1 ways. B) Adding a digit 0 at the end of an invalid string of length ...
SRWColAlg6_01_08
... and 4. • Rule 3 says that we can multiply (or divide) each side of an inequality by a positive number. • However, Rule 4 says that, if we multiply each side of an inequality by a negative number, then we reverse the direction of the inequality. ...
... and 4. • Rule 3 says that we can multiply (or divide) each side of an inequality by a positive number. • However, Rule 4 says that, if we multiply each side of an inequality by a negative number, then we reverse the direction of the inequality. ...
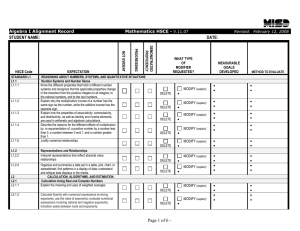
Solving Linear Inequalities in One Variable
... If unequal quantities are multiplied by the same positive quantity, the results will be unequal and in the same direction as the original inequality. If unequal quantities are multiplied by the same negative quantity, the results will be unequal but in the opposite direction of the original inequali ...
... If unequal quantities are multiplied by the same positive quantity, the results will be unequal and in the same direction as the original inequality. If unequal quantities are multiplied by the same negative quantity, the results will be unequal but in the opposite direction of the original inequali ...
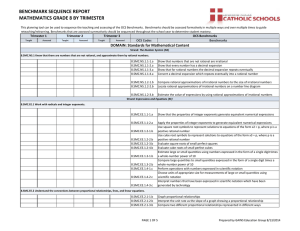
On the factorization of consecutive integers 1
... to show that the polynomial Lm (x) is irreducible for each integer m > 2 with m ≡ 2 (mod 4), whence, following the work of I. Schur [16, 17] and R. Gow [8], there is, for every integer m ≥ 2, a generalized Laguerre polynomial of degree m having Galois group the alternating group Am . The layout of t ...
... to show that the polynomial Lm (x) is irreducible for each integer m > 2 with m ≡ 2 (mod 4), whence, following the work of I. Schur [16, 17] and R. Gow [8], there is, for every integer m ≥ 2, a generalized Laguerre polynomial of degree m having Galois group the alternating group Am . The layout of t ...
Multiple-precision zero-finding methods and the complexity of
... From (3.1), the time required for a multiplication is negligible compared to the time for a function evaluation, if n ...
... From (3.1), the time required for a multiplication is negligible compared to the time for a function evaluation, if n ...