Numerical Simulation of Fracture in Viscoelastic Materials Based on
... The crack growth mechanism of elastomers is of great importance and interest in engineering applications, however, the correlation between numerical and theorical studies is not well established due to the complexity of the problem. The contribution presents an r-adaptive crack propagation scheme fo ...
... The crack growth mechanism of elastomers is of great importance and interest in engineering applications, however, the correlation between numerical and theorical studies is not well established due to the complexity of the problem. The contribution presents an r-adaptive crack propagation scheme fo ...
Mechanical Properties of Metals
... or a structure to withstand the forces applied to it For science point of view: what makes materials strong → helps us to design a better new one Learn basic concepts for metals, which have the simplest behavior Return to it later when we study ceramics, polymers, composite materials, nanotubes ...
... or a structure to withstand the forces applied to it For science point of view: what makes materials strong → helps us to design a better new one Learn basic concepts for metals, which have the simplest behavior Return to it later when we study ceramics, polymers, composite materials, nanotubes ...
A Combo Setup for Atmospheric Turbulence Measurements
... The fine-scale structure of turbulence is a largely unexplored aspect of the atmospheric boundary layer since it eludes conventional probing techniques. The direct measurement of fine structure using high resolution instruments such as hot-film or hotwire anemometers that can resolve smallest (dissi ...
... The fine-scale structure of turbulence is a largely unexplored aspect of the atmospheric boundary layer since it eludes conventional probing techniques. The direct measurement of fine structure using high resolution instruments such as hot-film or hotwire anemometers that can resolve smallest (dissi ...
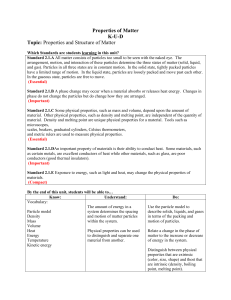
Properties of Matter - Red Clay Secondary Science Wiki
... arrangement, motion, and interaction of these particles determine the three states of matter (solid, liquid, and gas). Particles in all three states are in constant motion. In the solid state, tightly packed particles have a limited range of motion. In the liquid state, particles are loosely packed ...
... arrangement, motion, and interaction of these particles determine the three states of matter (solid, liquid, and gas). Particles in all three states are in constant motion. In the solid state, tightly packed particles have a limited range of motion. In the liquid state, particles are loosely packed ...
Problem Set #1 - Purdue College of Engineering
... hole (ie. gm/sec) ? 4. Given a velocity field u 2 xe x 3 ye y Kze z , where K is some constant and velocities are measured in m/s. Find the rate of expansion of a fluid particle (i.e. the fractional increase in volume per second). What value would K have to have for the fluid to be incompressi ...
... hole (ie. gm/sec) ? 4. Given a velocity field u 2 xe x 3 ye y Kze z , where K is some constant and velocities are measured in m/s. Find the rate of expansion of a fluid particle (i.e. the fractional increase in volume per second). What value would K have to have for the fluid to be incompressi ...
1 - vnhsteachers
... BASIC LAW OF FLUID PRESSURE The pressure at the bottom of a fluid can be expressed as: p = gh ( = density of fluid) (h = depth of fluid) (g = 9.8 m/s2) The pressure at any point in a fluid depends only on its density and its depth. It acts equally in all directions. ABSOLUTE PRESSURE The absolute ...
... BASIC LAW OF FLUID PRESSURE The pressure at the bottom of a fluid can be expressed as: p = gh ( = density of fluid) (h = depth of fluid) (g = 9.8 m/s2) The pressure at any point in a fluid depends only on its density and its depth. It acts equally in all directions. ABSOLUTE PRESSURE The absolute ...
Lecture 7 Mechanical Properties of Rocks
... on any given plane besides the principal stresses. In general, this is a three dimensional problem and can be done using mathematical tensors and vectors. In a special case where we can assume that the intermediate and minimum stresses are equal (for example below the ground surface), we can work ...
... on any given plane besides the principal stresses. In general, this is a three dimensional problem and can be done using mathematical tensors and vectors. In a special case where we can assume that the intermediate and minimum stresses are equal (for example below the ground surface), we can work ...
Max`sNotes
... This model is common in the mining industry, where ore is crushed and screened. Over sized particles are sent back around through the crusher as shown in model five. The equilibrium position is defined when the input to the system equals the output of the system. In the mineral processing industry t ...
... This model is common in the mining industry, where ore is crushed and screened. Over sized particles are sent back around through the crusher as shown in model five. The equilibrium position is defined when the input to the system equals the output of the system. In the mineral processing industry t ...
1 PHYSICS 231 Lecture 21: Some material science
... Stress: Tells something about the force causing the deformation Strain: Measure of the degree of deformation For small stress, strain and stress are linearly correlated. Strain = Constant*Stress Constant: elastic modulus The elastic modulus depends on: • Material that is deformed • Type of deformati ...
... Stress: Tells something about the force causing the deformation Strain: Measure of the degree of deformation For small stress, strain and stress are linearly correlated. Strain = Constant*Stress Constant: elastic modulus The elastic modulus depends on: • Material that is deformed • Type of deformati ...
Smart materials - 123SeminarsOnly.com
... Shape memory alloys or SMA's are metals that exhibit shape memory properties. It allows materials possessing shape memory properties to return to their original shape after having suffered some form of deformation after they are heated to temperatures above their transformation temperature. ...
... Shape memory alloys or SMA's are metals that exhibit shape memory properties. It allows materials possessing shape memory properties to return to their original shape after having suffered some form of deformation after they are heated to temperatures above their transformation temperature. ...
CombustionTeam080609
... To make a relationship between the Schlieren method and swirl number. ...
... To make a relationship between the Schlieren method and swirl number. ...
Fluids
... fluids. If a fluid is in motion it is useful to have an equation that relates the pressure to the velocity. If we assume, within the liquid: Viscous effects are negligible (so the “no slip” condition would not hold here) The flow is steady (no turbulence, no shock waves, etc.) The flow is inco ...
... fluids. If a fluid is in motion it is useful to have an equation that relates the pressure to the velocity. If we assume, within the liquid: Viscous effects are negligible (so the “no slip” condition would not hold here) The flow is steady (no turbulence, no shock waves, etc.) The flow is inco ...
AE1110x -‐ Lecture 3b -‐ The boundary layer on a flat plate In
... defined as the shear stress over the undisturbed dynamic pressure is equal to 0.664 divided by the squareroot of the local Reynolds number. So, the skin friction coefficient decreases w ...
... defined as the shear stress over the undisturbed dynamic pressure is equal to 0.664 divided by the squareroot of the local Reynolds number. So, the skin friction coefficient decreases w ...
The Role of Water in Controlling Metal Concentration in the Crust
... equilibria, then it follows that the chemistry of the fluids also must be controlled by mineral equilibria. The dominant ligand in most crustal fluids is chloride, since chloride behaves conservatively in all but halite-bearing rocks, fluid compositions can be evaluated to a first approximation for ...
... equilibria, then it follows that the chemistry of the fluids also must be controlled by mineral equilibria. The dominant ligand in most crustal fluids is chloride, since chloride behaves conservatively in all but halite-bearing rocks, fluid compositions can be evaluated to a first approximation for ...
Lecture 24 - Surface tension, viscous flow, thermodynamics
... reason they try to minimize the amount of surface energy that they have to waste. In a liquid which is falling through a gas, the smallest surface energy occurs when the fluid forms a spherical drop (e.g. a raindrop). However when a liquid drop is placed on a solid surface it may form different shap ...
... reason they try to minimize the amount of surface energy that they have to waste. In a liquid which is falling through a gas, the smallest surface energy occurs when the fluid forms a spherical drop (e.g. a raindrop). However when a liquid drop is placed on a solid surface it may form different shap ...
WHMIS
... 12. We commonly put gases or a mixture of gases and liquids under pressure so they will behave the way we want. For example, hair spray is a mixture of gas and liquid under pressure that produces a fine mist when releases. Think of 3 – 4 other examples of compressed gases or gases and liquids that y ...
... 12. We commonly put gases or a mixture of gases and liquids under pressure so they will behave the way we want. For example, hair spray is a mixture of gas and liquid under pressure that produces a fine mist when releases. Think of 3 – 4 other examples of compressed gases or gases and liquids that y ...
Slide 1 - Union College
... Many new devices and applications are being created that involve transporting droplets from one place to another. A common method of achieving this is through electrocapillary effects, a process through which a surface is electrowetted in such a way that it will cause a droplet to be pulled forward. ...
... Many new devices and applications are being created that involve transporting droplets from one place to another. A common method of achieving this is through electrocapillary effects, a process through which a surface is electrowetted in such a way that it will cause a droplet to be pulled forward. ...