JH WEEKLIES ISSUE #13 2011
... The Whole numbers are positive counting numbers; they are used to indicate the presence of whole objects or concepts, and can be used as ordinal numbers (i.e. 1st, 2nd, 3rd, etc.). Whole numbers include the numbers 0, 1, 2, 3… There is a closely-related set of numbers, the Natural numbers, that excl ...
... The Whole numbers are positive counting numbers; they are used to indicate the presence of whole objects or concepts, and can be used as ordinal numbers (i.e. 1st, 2nd, 3rd, etc.). Whole numbers include the numbers 0, 1, 2, 3… There is a closely-related set of numbers, the Natural numbers, that excl ...
1. Number Sense, Properties, and Operations
... a. Extend the properties of exponents to rational exponents. (CCSS: NRN) i. Explain how the definition of the meaning of rational exponents follows from extending the properties of integer exponents to those values, allowing for a notation for radicals in terms of rational exponents.1 (CCSS: N-RN.1) ...
... a. Extend the properties of exponents to rational exponents. (CCSS: NRN) i. Explain how the definition of the meaning of rational exponents follows from extending the properties of integer exponents to those values, allowing for a notation for radicals in terms of rational exponents.1 (CCSS: N-RN.1) ...
Chem_10_Resources_files/Scientific Measurement Ch397
... is considered significant 2. Zeroes between nonzero digits are significant 3. Leftmost zeroes appearing in front of nonzero digits are NOT significant 4. Zeroes at the end of numbers and to the right of a decimal point are always significant ...
... is considered significant 2. Zeroes between nonzero digits are significant 3. Leftmost zeroes appearing in front of nonzero digits are NOT significant 4. Zeroes at the end of numbers and to the right of a decimal point are always significant ...
MATH 2400: PRACTICE PROBLEMS FOR EXAM 1 1) Find all real
... the basic axioms (P0) through (P12) for ordered fields. In fact, in any ordered field which does not satisfy the Archimedean axiom, there exist infinitesimal elements S = {k ∈ Z+ | ...
... the basic axioms (P0) through (P12) for ordered fields. In fact, in any ordered field which does not satisfy the Archimedean axiom, there exist infinitesimal elements S = {k ∈ Z+ | ...
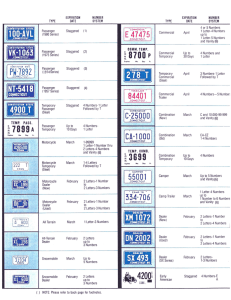
Connecticut License Plates (c.1980)
... 4 or 5 Numbers 1 Letter -4 Numbers up to 1 Letter -5 Numbers and Vanity (6) ...
... 4 or 5 Numbers 1 Letter -4 Numbers up to 1 Letter -5 Numbers and Vanity (6) ...