Mechanics 3 – Kinetics: A Level Maths Tutor
... mass, gravitational field strength(g) and the vertical distance the particle is above a fixed level. ...
... mass, gravitational field strength(g) and the vertical distance the particle is above a fixed level. ...
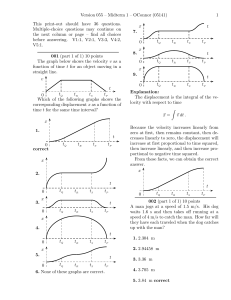
Version 055 – Midterm 1
... Find Sdown , the scale reading when the elevator is moving downward with constant velocity, in terms of Ss . 1. Sdown = 2. Sdown = 3. Sdown = 4. Sdown = 5. Sdown = ...
... Find Sdown , the scale reading when the elevator is moving downward with constant velocity, in terms of Ss . 1. Sdown = 2. Sdown = 3. Sdown = 4. Sdown = 5. Sdown = ...
“Here Comes the Sun” How the new
... contain mathematical treatments of various aspects of Newtonian celestial mechanics which purport to show the dynamic as well as the well-accepted kinematic equivalence of heliocentric and geocentric descriptions of the solar system. I show that not only does Sungenis fail to demonstrate this dynami ...
... contain mathematical treatments of various aspects of Newtonian celestial mechanics which purport to show the dynamic as well as the well-accepted kinematic equivalence of heliocentric and geocentric descriptions of the solar system. I show that not only does Sungenis fail to demonstrate this dynami ...
chapter8_PC
... event during which two particles come close to each other and interact by means of forces The time interval during which the velocity changes from its initial to final values is assumed to be short The interaction force is assumed to be much greater than any external forces present ...
... event during which two particles come close to each other and interact by means of forces The time interval during which the velocity changes from its initial to final values is assumed to be short The interaction force is assumed to be much greater than any external forces present ...
EXPERIMENT OF SIMPLE VIBRATION
... b) Frequency of free vibration changes with respect to the mass and spring coefficient. Compare the frequencies determined from the theory with those determined experimentally. Which error sources exits? What are the other differences between theoretical and experimental results? How are they explai ...
... b) Frequency of free vibration changes with respect to the mass and spring coefficient. Compare the frequencies determined from the theory with those determined experimentally. Which error sources exits? What are the other differences between theoretical and experimental results? How are they explai ...
Mechanics 3 Revision Notes
... Newton’s Law of Gravitation Tycho Brahe made many, many observations on the motion of planets. Then Johannes Kepler, using Brahe’s results, formulated Kepler’s laws of planetary motion. Finally Sir Isaac Newton produced his Universal Law of Gravitation, from which Kepler’s laws could be derived. ...
... Newton’s Law of Gravitation Tycho Brahe made many, many observations on the motion of planets. Then Johannes Kepler, using Brahe’s results, formulated Kepler’s laws of planetary motion. Finally Sir Isaac Newton produced his Universal Law of Gravitation, from which Kepler’s laws could be derived. ...
Newton`s Second Law of Motion
... Each component equation relates the forces on the object in that direction with the acceleration in that direction. A net force in the x direction will cause acceleration in the x direction. We will often just use the x and y directions in 2D. We will skip the vector notation when we are dealing wit ...
... Each component equation relates the forces on the object in that direction with the acceleration in that direction. A net force in the x direction will cause acceleration in the x direction. We will often just use the x and y directions in 2D. We will skip the vector notation when we are dealing wit ...
Circular motion review packet
... If we measure the period, T, the time needed for the object to make a complete revolution, we can calculate the speed of the object in UCM. During this time, it travels a distance equal to the circumference of the 2π r circle, 2πr, where r is the radius of the circular path. The object’s speed, then ...
... If we measure the period, T, the time needed for the object to make a complete revolution, we can calculate the speed of the object in UCM. During this time, it travels a distance equal to the circumference of the 2π r circle, 2πr, where r is the radius of the circular path. The object’s speed, then ...
Expanding Newton Mechanics with Neutrosophy and Quadstage
... principle of the uniqueness of truth, this paper presents the New Newton Mechanics (NNM) taking law of conservation of energy as unique source law with Neutrosophy and Quad-stage Method. In the area of Newton Mechanics, there should be one truth only. Other so-called truth, either it can be derived ...
... principle of the uniqueness of truth, this paper presents the New Newton Mechanics (NNM) taking law of conservation of energy as unique source law with Neutrosophy and Quad-stage Method. In the area of Newton Mechanics, there should be one truth only. Other so-called truth, either it can be derived ...
Mechanics - akamdiplomaphysics
... objects here on the earth due to friction Possible example could be a puck on ice where it is a near frictionless surface ...
... objects here on the earth due to friction Possible example could be a puck on ice where it is a near frictionless surface ...
Unit&3:Force
... A!picture!like!this!is!called!a!free!body!diagram.!!It!includes!only!a!system!of!interest,!and!the!forces!acting! on!it.!!Our!system!above!is!just&the&pen.!!In!Newtonian!physics,!all!forces!are!considered!as!arising!from!an! interaction!between!two!objects.!!Forces!are!specified!by!identifying!the!o ...
... A!picture!like!this!is!called!a!free!body!diagram.!!It!includes!only!a!system!of!interest,!and!the!forces!acting! on!it.!!Our!system!above!is!just&the&pen.!!In!Newtonian!physics,!all!forces!are!considered!as!arising!from!an! interaction!between!two!objects.!!Forces!are!specified!by!identifying!the!o ...
Modified Newtonian dynamics

In physics, modified Newtonian dynamics (MOND) is a theory that proposes a modification of Newton's laws to account for observed properties of galaxies. Created in 1983 by Israeli physicist Mordehai Milgrom, the theory's original motivation was to explain the fact that the velocities of stars in galaxies were observed to be larger than expected based on Newtonian mechanics. Milgrom noted that this discrepancy could be resolved if the gravitational force experienced by a star in the outer regions of a galaxy was proportional to the square of its centripetal acceleration (as opposed to the centripetal acceleration itself, as in Newton's Second Law), or alternatively if gravitational force came to vary inversely with radius (as opposed to the inverse square of the radius, as in Newton's Law of Gravity). In MOND, violation of Newton's Laws occurs at extremely small accelerations, characteristic of galaxies yet far below anything typically encountered in the Solar System or on Earth.MOND is an example of a class of theories known as modified gravity, and is an alternative to the hypothesis that the dynamics of galaxies are determined by massive, invisible dark matter halos. Since Milgrom's original proposal, MOND has successfully predicted a variety of galactic phenomena that are difficult to understand from a dark matter perspective. However, MOND and its generalisations do not adequately account for observed properties of galaxy clusters, and no satisfactory cosmological model has been constructed from the theory.