Download Chapter 7

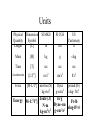
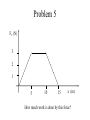
Chapter 7 - Work and Energy
• Work
– Definition of Work [units]
– Work done by a constant force (e.g friction,weight)
– Work done by a varying force (e.g. a spring)
– Work in 3 dimensions – General Definition
• Work and Kinetic Energy
– Definition of Kinetic Energy
– Work-Energy Principle
Definitions
• Work - The means of
transferring energy by the
application of a force.
• Work is the product of the
magnitude of displacement
times the component of
that force in the direction
of the displacement.
• Work is a scalar
• Energy - The state of one
or more objects. A scalar
quantity, it defines the
ability to do work.
W  F//  r  F  r cos 
Units
Physical
Quantity
Length
Dimension
Symbol
[L]
SI MKS
SI CGS
m
cm
US
Customary
ft
Mass
[M]
kg
g
slug
Time
[T]
sec
sec
sec
Acceleration
[L/T2]
m/s2
cm/s2
ft/s2
Dyne
g-cm/s2
pound (lb)
slug- ft/s2
Force
[M-L/T2] newton (N)
kg-m/s2
Energy [M-L2/T2] Joule (J)
N-m
kg-m2/s2
Erg
Ft-lb
Dyne-cm
2/s2
slug-ft
g-cm2/s2
Problem 1
• A 1500 kg car accelerates uniformly from
rest to a speed of 10 m/s in 3 s.
• Find the work done on the car in this time
W  F//  r  F  r cos 
How much work is done by this guy?
Walking at a constant speed
r
W  F//  r  F  r cos 
Problem 3
•
•
•
•
•
m = 50 kg
displacement = 40 m
force applied = 100 N
37o angle wrt floor
mk = 0.1
• Find net work done
moving the crate
Vector Multiplication – Scalar Product
A B  A B cos 
ˆi ˆi  ˆj ˆj  kˆ kˆ  1
ˆi ˆj  ˆi kˆ  ˆj kˆ  0
A  A x ˆi  A y ˆj  A z kˆ
B  Bx ˆi  By ˆj  Bz kˆ
A B  A x Bx  A y By  A z Bz
A more elegant definition for work
W  F//  r  F  r cos 
A B  A B cos 
W  F r
Problem 4
• How much work is done pulling the wagon 100 m
in the direction shown by the boy applying the
force:
F  17Niˆ  10Njˆ
r
Work done by a varying force
7
W   Fi cos i li
W1  F1 cos 1l1
i 1
7
b
b
i 1
a
a
W  lim  Fi cos i li   Fcos dl   F  dl
li 0
Work in three dimensions
F  Fx ˆi  Fy ˆj  Fz kˆ
dr  dxiˆ  dyjˆ  dzkˆ
b
xb
yb
zb
a
xa
ya
za
W   F  dr   Fx dx   Fy dy   Fz dz
Problem 5
Fx (N)
3
2
1
5
10
15
x (m)
How much work is done by this force?
Hooke’s Law and
the work to compress/extend a spring
Fs  kx
b
xb
a
xa
W   F  dr   Fx dx
WP  
xb x
xa 0
1 2
 kx  dx  kx
2
Kinetic Energy and the
Work-Energy Principle
v2  v02
1
1
2
W F d ma d m
d  mv  mv02
2d
2
2
W  K  K 0  K
1
K  mv 2
2
And you can show this with calculus too!
b
xb
a
xa
W   F  dr   Fx dx
W
2
1
2
2
dv
dx
1
1
2
m dx   m dv   mvdv  mv 2  mv12
1
1
dt
dt
2
2
Problem 6
•
•
•
•
•
A 3 kg mass has an initial velocity, v = (5i - 3j) m/s.
What is the kinetic energy at this time?
The velocity changes to (8i + 4j) m/s.
What is the change in kinetic energy?
How much work was done?
Problem 7
• A 2 kg block is attached to a light spring of force constant
500 N/m. The block is pulled 5 cm to the right and of
equilibrium. How much work is required to move the
block?
• If released from rest, find the speed of the block as it
passes back through the equilibrium position if
– the horizontal surface is frictionless.
– the coefficient of friction is 0.35.