Download GATE

Quantum Computer Simulation
Alex Bush
Matt Cole
James Hancox
Richard Inskip
Jan Zaucha
Aims
 Develop an understanding of quantum computing
 Implement a simulation of a quantum computer
 Simulate Grover’s algorithm using our implementation
of a quantum computer
 Learn group work skills and techniques
Background
 Feynman – 1982
 Deutsch – 1994
 Shor – 1994
 Grover – 1996
Qubits
 Classically 0 or 1
 Quantum bits: qubits
 Information obtained by measurement
Register: System of Qubits
 For n qubits 2n states
 Basis vectors by convention in binary notation
Example : basis states for a 3 qubit register
Gates
 Unitary linear operators which act on the register to
alter its state
 Universal set of gates:
 Single qubit


Hadamard
Phase
 Two qubit

CNOT
Quantum Algorithms
 Ingredients: registers, universal set of gates
 Advantage over classical computations: quantum
interference
Grover’s Algorithm
 1996, Lov Grover
 Search problem: find particular element in an
unordered list of N entries
 Need to be able to assess if search found correct
element, all elements in list have to be known
beforehand
Implementation of the
Quantum Computer
 Register – the register is implemented as a matrix
of complex numbers
 Gate – gates are implemented in both matrix and
functional form
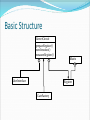
Basic Structure
GroverCircuit
prepareRegister()
nextIteration()
measureRegister()
Matrix
UserInterface
Register
GateFactory
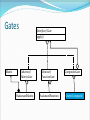
Gates
{interface} Gate
apply()
Matrix
{abstract}
MatrixGate
HadamardMatrix
{abstract}
FunctionGate
HadamardFunction
CompositeGate
GroverComposite
UML Diagram
Grover Iteration
The GroverComposite gate is a special gate that
when applied to the register performs a Grover
iteration.
groverIteration[0] = oracle;
groverIteration[1] =
hadamardTransform;
groverIteration[2] = nand;
groverIteration[3] =
hadamardTransform;
Implementation:
 The Quantum Register,
 Quantum Gates;
- Matrix,
- Function,
- Composite,
 Factory Method for creating Gates,
 Quantum Algorithm and the GUI.
Implementation: Register
 The Quantum Register:



An extension of the Matrix class,
2N entries,
A storage medium for the Probability Amplitudes of each state.
 An example of a 2-qubit register:
a |0> + b|1>
c |0> + d|1>
ac|00> + ad|01> + bc|10> + bd|11>
|ac|
|ad|
|bc|
|bd|
Implementation: Gates
 A Quantum Gate:

Gates were implemented in a variety of ways:
 Matrix
 Functional
 Composite

Gates were packaged with a private constructor to make use of
a factory method for creating the gates.
Implementation: Gates
 1-qubit Matrix Gate;


A specific 2x2 matrix was constructed to perform a single bit
operation depending on the role of the gate.
This could then be extended by applying(tensor product)
Identity matrices to the 2x2 gate.
 An example of such would be to apply a “GATE” to a 4-
qubit register, with the qubit to be operated on being the
second:
Implementation: Gates
 Higher order Matrix Gates and Functional Gates:

Both for higher order matrix gates and functional gates a
defined method was not so obvious for the operation of the
gates.

The use of patterns were used to analysis the expected change
on the register and a matrix or function created from this.

Functional gates using Java operations such as bitwise shift
operators.
Implementation: Factory
 Factory method is an abstract class which can be used to
create gates – matrix or functional – all from one
location.
 All Gate constructors are private, therefore can only be
created from inside the Factory.
 The factory allows control over all gates being matrix or
functional or overloading certain gates to a different
representation if desired..
Implementation:
 Quantum Algorithm and the GUI;





The algorithm and GUI sections of the code are unique to
Grover’s algorithm.
When the GUI is run it prompts the user for specific values
such as register size and the element to search for in the
register.
The register is then prepared by applying a Hadamart gate to
every qubit.
Iterations of Grover’s are then applied to the register.
A measurement can then be taken.
Demonstration
Need for managment tools
 Share code between members
 Ensure members have up-to-date copies of files
 Backups of previous versions
Version control systems
Subversion (SVN)
 Widely used – high compatability
 Free and open-source
 Integrates well with Eclipse
 Central repository for files
 Full version history of files
SVN (cont.)
Check out
Me
Edit files
Repository
Check in
Me
Check out
Check out
Jan
Me
Edit files
Edit files
Check in
Repository
Update
Me
Jan
Merge Changes
Check in
Me
Google Code
 Provide SVN service
 View file diffs online (changes in files between versions)
 Mailing list
 Issues/bug tracker
 File hosting
Eclipse
 GUI to develop under
 Code completion
 Speed up routine operations
 Automatically compiles code
 Graphical interface for SVN (Subclipse)
Conclusion
 All of our aims achieved
 Scope for further work using existing code
 Improved team work skills
 Improved programming skills