Download Physics Midterm Study Guide

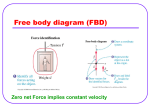
Physics Midterm Study Guide 2014
Unit 1 – Basics
Base units in Mechanics are meters, kilograms, and seconds (Kelvins, moles amperes and candelas are base units too)
Derived units – combinations of base units, for example, m/s
Metric prefixes – tera, giga, mega, kilo, deci, milli, micro, nano, pico
Measurements
Proper measurements consist of the certain digits from scaled increments and one uncertain (estimated) digit
Measurement uncertainty – no measurement is completely true, because two things are always less than perfect::
Precision – exactness or fineness of a measurement; how close the scale markings are
Precision is limited by the design of the measuring instrument
Accuracy – closeness of a measurement to the true value
Accuracy is limited by the original quality of the instrument, wear and tear, and errors in its use.
Both of these two terms can be used to describe either a measuring instrument or a measurement.
Scientific notation arithmetic
For addition or subtraction units must be the same. For multiplication and division they can be different.
Know how to enter powers of 10 in calculations reliably in your calculator
Dependent and independent variables in an experiment are the only ones we want to allow to change
Position, x , is the distance and direction from the origin. It is in bold font because its direction is important
Displacement, Δx , is the distance and direction between two positions given by Δx = xf - xi
Clock reading, t is what a stopwatch or other timer indicates at any instant.
Time interval, Δt , is the amount of time between clock readings given by Δt = tf - ti
Note that direction has no meaning for time, it’s a scalar quantity, so it is not in bold font.
Unit 2 – The Constant Velocity (CV) model
Constant velocity is motion characterized by equal displacements in equal time intervals
Representations of the CV model
Mathematical representation (equations)
v = Δx / Δt defines average velocity as the displacement of an object divided by the time it traveled.
The direction of v is important and must be specified
[Note: average speed, s, is defined by s = d / Δt , where d is the distance traveled.
The direction of s is not important]
Any other arrangement of v = Δx / Δt can also be called a mathematical representation of CV.
For example, xf = xi + v Δt comes from substituting xf - xi for Δx, then solving for xf
Graphical representations
Position vs. time (x-t) graph
On an x-t graph the slope of the line of best fit represents the velocity of the object
For constant velocity, the line of best fit on an x-t graph is a straight line with constant slope
Velocity vs. time (v-t) graph
On a v-t graph, the area under the line of best fit represents displacement
However, a v-t graph shows no information about position
Motion map representation
Consists of dots representing the position of the object at the end of equal time intervals, arranged in
sequence just above or below an arrow representing the x-axis and the positive direction. Arrows
(vectors) are added between the dots, whose lengths represent the velocities between positions.
Stacked dots represent no movement. Hollow dots represent instantaneous change in direction
x+
x+
t
Average velocity (and average speed, mentioned above) are general ideas that apply to all motion, not just CV
The average velocity of any object is its displacement divided by the total time it took, including rest time.
The length or shape of the path traveled, or changes in speed during the trip are not relevant.
Its defining equation is v = Δx / Δt
You should know and understand all of the above, and be able to:
 describe the motion of an object by interpreting its x-t and/or v-t graph
 produce two more representations of constant velocity motion when given one

work with all variations of the mathematical representation
Unit 3 – Uniform Acceleration (UA) Model
acceleration (a vector quantity) the rate of change of velocity a = Δv / Δt
the acceleration due to gravity on earth (g) is equal to 9.8 m/s2
x-t graph - unless the acceleration is zero (CV), the graph is a parabolic curve
the slope of the tangent to the curve at any point is the instantaneous velocity of the object at that time
v-t graph – the graph is a straight line
the slope of the v-t graph represents the acceleration of the object
mathematical model of UA is the four motion equations. They are derived from the graphical model
vf = vi + aΔt
Δx = ½ (vi + vf)
Δx = viΔt + ½ aΔt2
vf2 = vi2 + 2a Δx
Unit 4 – Free Particle Model
resolving vectors into x and y components
put the tail of the vector at the origin of an x-y coordinate system
measure the angle from the positive x-axis to the vector. This is called the “standard position”
the vector, the x-component and the y-component form a right triangle
the height of the triangle is the y-component
it is equal to the magnitude of the vector times the sine of the angle
the base of the triangle is the x-component. Use the cosine of the angle to find it
it is equal to the magnitude of the vector times the cosine of the angle
adding vectors
the vector sum of two vectors is called the resultant. R
resolve both vectors into their x and y components
add those components to get the x and y components of the resultant vector, Rx and Ry
use the Pythagorean theorem to get the magnitude of the resultant, R = (Rx2 + Ry2)1/2
use the inverse tangent to find the direction of R θR = tan-1 (Ry / Rx)
inertia – the tendency of an object to resist change in velocity
Inertia a property of mass
particle – a point mass representing the mass of an object.
system – a particle or group of particles whose behavior is of interest We define the system as we wish
surroundings – everything in the environment that is not part of the system
force (a vector quantity) F force is an interaction between two objects (or particles)
there are two types of forces
long range forces – pushes or pulls with no physical contact
examples are gravity, electrostatic and magnetic forces
contact forces – direct pushes or pulls due to physical contact
examples are tension, normal force, static friction, kinetic friction and spring forces
the unit of force is the Newton (N). one Newton = one kg-m/s2
normal force (FN or N ) – the force exerted on an object by a surface, always in a direction perpendicular to the surface
tension force (FT or T) – the force in a string, rope or cord
net force (ΣF or as called in some books, Fnet) – the vector sum of all the forces acting on an object
The net force can be calculated in the x and y directions separately ΣFx ΣFy
kinetic friction Fk force between two sliding surfaces, always in direction opposite to the motion
static friction Fa force between two surfaces that are not moving, always in the direction to resist motion
force diagram
represent the system as a dot
draw as vectors with tails on the dot all of the forces acting on the system from the surroundings
Newton’s first law – if there is no unbalanced force on an object (ΣF = 0), its velocity doesn’t change.
so, if an object’s velocity doesn’t change, there is no unbalanced force (ΣF = 0)
also, if an object’s velocity does change, there must be an unbalanced force (ΣF ≠ 0)
Newton’s first law can be applied to the x and y directions separately
if velocity is constant in the x-direction then ΣFx = 0
if velocity is constant in the y-direction then ΣFy = 0
Newton’s third law – forces always occur in pairs (sometimes called action/reaction pairs, but that is bad terminology)
the two forces are equal in magnitude, but opposite in direction
FB on A = - FA on B
to identify the other force in a pair use a verbal pattern like “earth pulls on ball - ball pulls on earth”
note that they act on two different objects, A and B
therefore, “rope pulls on box with a force – floor exerts equal friction force on box” is not a force pair
Unit 5 – Constant Net Force Model
Newton’s 2nd law of motion: a = ΣF / m
We use this equation to find either m, a, ΣF, or one of the forces included in ΣF
Friction
kinetic friction force between two specific materials can be calculated as Fk = µkFn where µk is an empirically
determined dimensionless constant for the two surface materials, and is called the coefficient of kinetic friction.
Static friction force between two specific materials can be calculated as Fs = µsFn where µs is an empirically
determined dimensionless constant for the two surface materials, and is called the coefficient of static friction
Unit 6 – 2D Motion Model
projectile – an object in motion whose path is affected by the force of gravity
key concept: the horizontal and vertical motion of an object are independent of (not affected by) each other
To analyze projectile motion, realize that
the horizontal motion is straight line motion that can be analyzed using the kinematic equations
the velocity in the horizontal direction is constant (if air resistance is neglected)
therefore, vxi , vxf and vx are all the same in the horizontal direction
for horizontal motion, Δx = vi cosθ Δt is the only equation needed
the vertical motion is straight line motion that can be analyzed using the kinematic equations
the velocity in the vertical direction is accelerated by gravity. ay = -9.8 m/s2
therefore, vyi , vyf and vy all have different values in the vertical direction
for vertical motion, any of the four motion equations apply, but the most useful are usually
vyf = vyi + a Δt , which gives Δt = 2 vyi / 9.8 when (and only when) Δy = 0
and Δy = vyi Δt + ½ ay Δt2
Δt is the same for for the objects horizontal and vertical motion
For the midterm you should be able to
Answer questions regarding any of the definitions and concepts above
Create and analyze x-t and v-t graphs to understand what the object is doing
Draw correct force diagrams for situations you are asked to analyze
Use the four motion equations and Newton’s three laws together to solve problems
Expect:
Three parts to the exam:
25 common assessment multiple choice questions
50 honors multiple choice / true-false / matching questions
6 - 7 multi-part problems of the type
vector addition
kinematics (“fab four” equations)
horizontally launched projectile
angled projectile
Balanced forces (Newton’s 1st Law)
Newton’s 2nd law, including
horizontal motion, with friction
on a ramp with friction
in an elevator with apparent weight (we will cover this)