![[2014 solutions]](http://s1.studyres.com/store/data/008843334_1-6541359c94dca59dbb1b50426f79633e-300x300.png)
Full text
... A rational number r is said to be divisible by a prime number p provided the numerator of r is divisible by p . Here it is assumed that all rational numbers are written in standard form. That is, the numerators and denominators are relatively prime integers and the denominators are positive. Certain ...
... A rational number r is said to be divisible by a prime number p provided the numerator of r is divisible by p . Here it is assumed that all rational numbers are written in standard form. That is, the numerators and denominators are relatively prime integers and the denominators are positive. Certain ...
polynomial function in x of degree n
... If a is a real number than the following statements are equivalent: • x= a is a real zero of the function • X = a is a solution of the polynomial equation f(x) = 0 • (x-a) is a factor of the polynomial f(x). • (a,0) is an x-intercept of the graph of f(x). ...
... If a is a real number than the following statements are equivalent: • x= a is a real zero of the function • X = a is a solution of the polynomial equation f(x) = 0 • (x-a) is a factor of the polynomial f(x). • (a,0) is an x-intercept of the graph of f(x). ...
Markov, Chebyshev, and the Weak Law of Large Numbers
... Markov, Chebyshev, and the Weak Law of Large Numbers The Law of Large Numbers is one of the fundamental theorems of statistics. One version of this theorem, The Weak Law of Large Numbers, can be proven in a fairly straightforward manner using Chebyshev's Theorem, which is, in turn, a special case of ...
... Markov, Chebyshev, and the Weak Law of Large Numbers The Law of Large Numbers is one of the fundamental theorems of statistics. One version of this theorem, The Weak Law of Large Numbers, can be proven in a fairly straightforward manner using Chebyshev's Theorem, which is, in turn, a special case of ...
Prime Numbers and How to Avoid Them
... Proof Concluded The “Chinese Remainder Theorem” guarantees we can find infinitely many such numbers. The smallest is k= 201 44650 31451 65117 This is a “Sierpinski number”, which makes every term in the infinite sequence composite. Half are divisible by 3, a quarter divisible by 5, etc. ...
... Proof Concluded The “Chinese Remainder Theorem” guarantees we can find infinitely many such numbers. The smallest is k= 201 44650 31451 65117 This is a “Sierpinski number”, which makes every term in the infinite sequence composite. Half are divisible by 3, a quarter divisible by 5, etc. ...
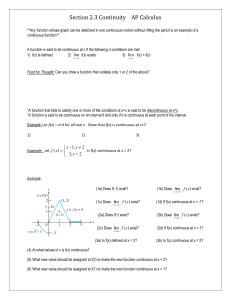
ap calculus 20 week review part iii2
... f is discontinuous only at x=-2 f is discontinuous only at x =1 If f (-2) is defined to be 4, then f will be continuous everywhere f is continuous everywhere f is discontinuous at x=-2 and at x=1. ...
... f is discontinuous only at x=-2 f is discontinuous only at x =1 If f (-2) is defined to be 4, then f will be continuous everywhere f is continuous everywhere f is discontinuous at x=-2 and at x=1. ...
Fundamental theorem of calculus
The fundamental theorem of calculus is a theorem that links the concept of the derivative of a function with the concept of the function's integral.The first part of the theorem, sometimes called the first fundamental theorem of calculus, is that the definite integration of a function is related to its antiderivative, and can be reversed by differentiation. This part of the theorem is also important because it guarantees the existence of antiderivatives for continuous functions.The second part of the theorem, sometimes called the second fundamental theorem of calculus, is that the definite integral of a function can be computed by using any one of its infinitely-many antiderivatives. This part of the theorem has key practical applications because it markedly simplifies the computation of definite integrals.