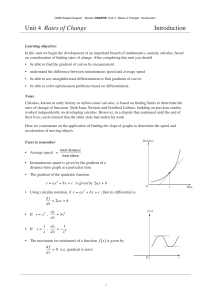
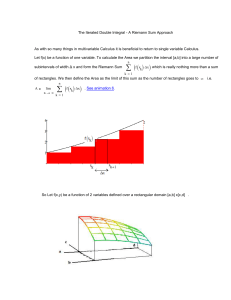
4. Growth of Functions 4.1. Growth of Functions. Given functions f
... that f is big-O of g expresses the fact that for large enough x, f will be bounded above by some constant multiple of g. Theorem 4.2.1 gives a necessary condition for f to be big-O of g in terms of limits. The two notions aren’t equivalent since there are examples where the definition holds, but the ...
... that f is big-O of g expresses the fact that for large enough x, f will be bounded above by some constant multiple of g. Theorem 4.2.1 gives a necessary condition for f to be big-O of g in terms of limits. The two notions aren’t equivalent since there are examples where the definition holds, but the ...
Unit 3 Items to Support Formative Assessment
... Consider the function f(x) = 2x2 + 3x + 4 a. How many complex solutions does the function f(x) have? Explain your reasoning. b. Find all the solutions to the function. Answer: a. The function has two complex solutions, according to the Fundamental Theorem of Algebra. The function has a degree of 2, ...
... Consider the function f(x) = 2x2 + 3x + 4 a. How many complex solutions does the function f(x) have? Explain your reasoning. b. Find all the solutions to the function. Answer: a. The function has two complex solutions, according to the Fundamental Theorem of Algebra. The function has a degree of 2, ...
End of Year Review Hmwk
... Condense each expression to a single logarithm. log 6 50. ln 8 − 2 ln 2 49. 2 log 3 7 + 33 ...
... Condense each expression to a single logarithm. log 6 50. ln 8 − 2 ln 2 49. 2 log 3 7 + 33 ...
![[2014 question paper]](http://s1.studyres.com/store/data/008844916_1-6bcf832b30821138ae4b8d8f7d9aa434-300x300.png)
Semester Review
... always three times the radius. At what rate is the radius increasing when the height is 4 ft? ...
... always three times the radius. At what rate is the radius increasing when the height is 4 ft? ...
![[Part 1]](http://s1.studyres.com/store/data/008795849_1-075cc9ba198c265a8a5f7353865fded1-300x300.png)
PERMUTATIONS WITHOUT 3-SEQUENCES 1. Introduction, The
... to this set of sequences. More recently, Kaplansky [2] and Wolfowitz [4] have enumerated permutations without rising or falling 2-sequences, that is, without 21,32, • • • ,n n — l a s w e l l a s 12, • • -,w —1 n. An addition to these results, the enumeration of permutations without 3-sequences, 123 ...
... to this set of sequences. More recently, Kaplansky [2] and Wolfowitz [4] have enumerated permutations without rising or falling 2-sequences, that is, without 21,32, • • • ,n n — l a s w e l l a s 12, • • -,w —1 n. An addition to these results, the enumeration of permutations without 3-sequences, 123 ...
Fundamental theorem of calculus
The fundamental theorem of calculus is a theorem that links the concept of the derivative of a function with the concept of the function's integral.The first part of the theorem, sometimes called the first fundamental theorem of calculus, is that the definite integration of a function is related to its antiderivative, and can be reversed by differentiation. This part of the theorem is also important because it guarantees the existence of antiderivatives for continuous functions.The second part of the theorem, sometimes called the second fundamental theorem of calculus, is that the definite integral of a function can be computed by using any one of its infinitely-many antiderivatives. This part of the theorem has key practical applications because it markedly simplifies the computation of definite integrals.