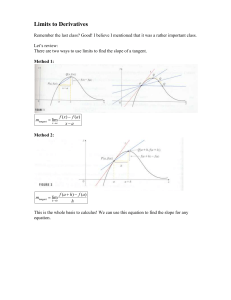
Limits to Derivatives
... derivative. The derivative is a function that represents the slope of a function at any point. We use two main ways to represent a function. The derivative of a function f(x) is f’(x) [we say: “f prime of x” or simply “the derivative of f”]. df (x) dy Another way to represent the derivative of the r ...
... derivative. The derivative is a function that represents the slope of a function at any point. We use two main ways to represent a function. The derivative of a function f(x) is f’(x) [we say: “f prime of x” or simply “the derivative of f”]. df (x) dy Another way to represent the derivative of the r ...
Notes on the large sieve
... results rested on an underlying analytic inequality on sums of squares of values of a trigonometric polynomial. This was first formulated explicitly by Davenport and Halberstam [DH] in 1966, amd has come to be known as the “analytic large sieve inequality”. Later writers have refined this result by ...
... results rested on an underlying analytic inequality on sums of squares of values of a trigonometric polynomial. This was first formulated explicitly by Davenport and Halberstam [DH] in 1966, amd has come to be known as the “analytic large sieve inequality”. Later writers have refined this result by ...
Fundamental theorem of calculus
The fundamental theorem of calculus is a theorem that links the concept of the derivative of a function with the concept of the function's integral.The first part of the theorem, sometimes called the first fundamental theorem of calculus, is that the definite integration of a function is related to its antiderivative, and can be reversed by differentiation. This part of the theorem is also important because it guarantees the existence of antiderivatives for continuous functions.The second part of the theorem, sometimes called the second fundamental theorem of calculus, is that the definite integral of a function can be computed by using any one of its infinitely-many antiderivatives. This part of the theorem has key practical applications because it markedly simplifies the computation of definite integrals.