f ``(x)
... Relative Extrema RELATIVE MAXIMUM OR MINIMUM Let c be a number in the domain of a function f. Then f(c) is a relative maximum for f if there exists an open interval (a, b) containing c such that f(x) f(c) for all x in (a, b) f(c) is a relative minimum for f if there exists an open interval (a ...
... Relative Extrema RELATIVE MAXIMUM OR MINIMUM Let c be a number in the domain of a function f. Then f(c) is a relative maximum for f if there exists an open interval (a, b) containing c such that f(x) f(c) for all x in (a, b) f(c) is a relative minimum for f if there exists an open interval (a ...
Full text
... 2 and 3 can be viewed as a binary sequence. The numbers 2 and 3 are the component factors of this binary. This paper explores the combination of these components to form the properties of the integers in the binary. Properties considered are: value, ordinality (position in the sequence), and exponen ...
... 2 and 3 can be viewed as a binary sequence. The numbers 2 and 3 are the component factors of this binary. This paper explores the combination of these components to form the properties of the integers in the binary. Properties considered are: value, ordinality (position in the sequence), and exponen ...
Exam 1 Study Guide MA 111 Spring 2015 It is suggested you review
... (22) Perform the following computations in S5 : (a) [1 2 3] [2 5 4] (b) [1 2] [2 3] [3 5] [5 4] (23) Let g = [1 2 3 4 5 6][7 8 9] in S9 . (a) Let t = [2 5]. Draw convincing pictures to show how the cycle number of g ◦ t differs from the cycle number of g. (b) Let t = [4 8]. Draw convincing pictures ...
... (22) Perform the following computations in S5 : (a) [1 2 3] [2 5 4] (b) [1 2] [2 3] [3 5] [5 4] (23) Let g = [1 2 3 4 5 6][7 8 9] in S9 . (a) Let t = [2 5]. Draw convincing pictures to show how the cycle number of g ◦ t differs from the cycle number of g. (b) Let t = [4 8]. Draw convincing pictures ...
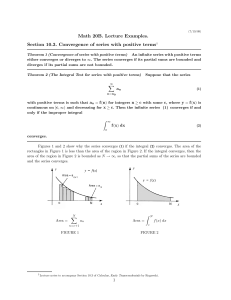
Math 20B. Lecture Examples. Section 10.3. Convergence of series
... Figures 1 and 2 show why the series converges (1) if the integral (2) converges. The area of the rectangles in Figure 1 is less than the area of the region in Figure 2. If the integral converges, then the area of the region in Figure 2 is bounded as N → ∞, so that the partial sums of the series are ...
... Figures 1 and 2 show why the series converges (1) if the integral (2) converges. The area of the rectangles in Figure 1 is less than the area of the region in Figure 2. If the integral converges, then the area of the region in Figure 2 is bounded as N → ∞, so that the partial sums of the series are ...
educative commentary on jee 2014 advanced mathematics papers
... in the present case. At any rate, we are not asked to identify the real roots but only to test some statements about the numbers of real roots (as opposed to the roots themselves). So methods from calculus have to be used and often the answers are obtained by merely looking at a (well-drawn) graph. ...
... in the present case. At any rate, we are not asked to identify the real roots but only to test some statements about the numbers of real roots (as opposed to the roots themselves). So methods from calculus have to be used and often the answers are obtained by merely looking at a (well-drawn) graph. ...
Prime-perfect numbers - Dartmouth Math Home
... many of the most interesting problems remain unsolved. Chief among them is the question of whether or not there are infinitely many multiply perfect numbers. In this note we introduce a class of numbers whose definition is inspired by the perfect numbers but for which we can prove that there are inf ...
... many of the most interesting problems remain unsolved. Chief among them is the question of whether or not there are infinitely many multiply perfect numbers. In this note we introduce a class of numbers whose definition is inspired by the perfect numbers but for which we can prove that there are inf ...
Utility maximization in affine stochastic volatility models
... Remark 2.6 Since only the derivative u0 appears in this criterion, the same result except for (2.1) can be applied to logarithmic utility by setting p = 1. Since in this case LV (ϕ)1−p is supposed to be a martingale, the only possible choice is L = 1. Hence the sufficient condition of Corollary 2.5 ...
... Remark 2.6 Since only the derivative u0 appears in this criterion, the same result except for (2.1) can be applied to logarithmic utility by setting p = 1. Since in this case LV (ϕ)1−p is supposed to be a martingale, the only possible choice is L = 1. Hence the sufficient condition of Corollary 2.5 ...
Fundamental theorem of calculus
The fundamental theorem of calculus is a theorem that links the concept of the derivative of a function with the concept of the function's integral.The first part of the theorem, sometimes called the first fundamental theorem of calculus, is that the definite integration of a function is related to its antiderivative, and can be reversed by differentiation. This part of the theorem is also important because it guarantees the existence of antiderivatives for continuous functions.The second part of the theorem, sometimes called the second fundamental theorem of calculus, is that the definite integral of a function can be computed by using any one of its infinitely-many antiderivatives. This part of the theorem has key practical applications because it markedly simplifies the computation of definite integrals.