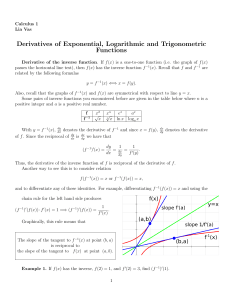
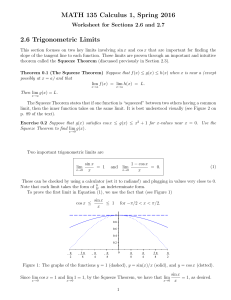
Convex Programming - Santa Fe Institute
... A subset C of a Euclidean space is convex if it contains the line segment connecting any two of its members. That is, if x and y are vectors in C and t is a number between 0 and 1, the vector tx + (1 − t)y is also in C. A linear combination with non-negative weights which sum to 1 is a convex combin ...
... A subset C of a Euclidean space is convex if it contains the line segment connecting any two of its members. That is, if x and y are vectors in C and t is a number between 0 and 1, the vector tx + (1 − t)y is also in C. A linear combination with non-negative weights which sum to 1 is a convex combin ...
Fundamental theorem of calculus
The fundamental theorem of calculus is a theorem that links the concept of the derivative of a function with the concept of the function's integral.The first part of the theorem, sometimes called the first fundamental theorem of calculus, is that the definite integration of a function is related to its antiderivative, and can be reversed by differentiation. This part of the theorem is also important because it guarantees the existence of antiderivatives for continuous functions.The second part of the theorem, sometimes called the second fundamental theorem of calculus, is that the definite integral of a function can be computed by using any one of its infinitely-many antiderivatives. This part of the theorem has key practical applications because it markedly simplifies the computation of definite integrals.