1. Geometry Objectives complete
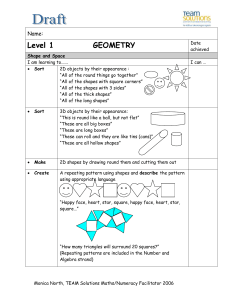
... “All of the shapes with square corners” “All of the shapes with 3 sides” “All of the thick shapes” “All of the long shapes” ...
... “All of the shapes with square corners” “All of the shapes with 3 sides” “All of the thick shapes” “All of the long shapes” ...
UNIT PLAN TEMPLATE
... Big Idea/Theme: The physical world can be described by understanding the connection between the identification of basic attributes and the classification of two-dimensional shapes. ...
... Big Idea/Theme: The physical world can be described by understanding the connection between the identification of basic attributes and the classification of two-dimensional shapes. ...
LESSON 4-1: CONGRUENT FIGURES/POLYGONS
... LESSON 4-1: CONGRUENT FIGURES/POLYGONS Examples of Polygons ...
... LESSON 4-1: CONGRUENT FIGURES/POLYGONS Examples of Polygons ...
8-1. PINWHEELS AND POLYGONS Inez loves pinwheels. One day
... form convex polygons while others result in non-convex polygons? Consider this as you answer the following questions. ...
... form convex polygons while others result in non-convex polygons? Consider this as you answer the following questions. ...
Triangles
... What are 2-Dimensional Shapes? A 2-dimensional shape is a geometric figure that has length and width but no thickness or depth. It is a shape that is flat. There are 2Dimensional shapes everywhere! Point to a few of them in the classroom. ...
... What are 2-Dimensional Shapes? A 2-dimensional shape is a geometric figure that has length and width but no thickness or depth. It is a shape that is flat. There are 2Dimensional shapes everywhere! Point to a few of them in the classroom. ...
Name - Harmony
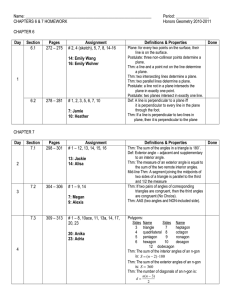
... Definitions & Properties Thm: The sum of the angles in a triangle is 180˚. Def: Exterior angle – adjacent and supplementary to an interior angle. Thm: The measure of an exterior angle is equal to the sum of the two remote interior angles. Mid-line Thm: A segment joining the midpoints of two sides of ...
... Definitions & Properties Thm: The sum of the angles in a triangle is 180˚. Def: Exterior angle – adjacent and supplementary to an interior angle. Thm: The measure of an exterior angle is equal to the sum of the two remote interior angles. Mid-line Thm: A segment joining the midpoints of two sides of ...
Tessellation

A tessellation of a flat surface is the tiling of a plane using one or more geometric shapes, called tiles, with no overlaps and no gaps. In mathematics, tessellations can be generalized to higher dimensions and a variety of geometries.A periodic tiling has a repeating pattern. Some special kinds include regular tilings with regular polygonal tiles all of the same shape, and semi-regular tilings with regular tiles of more than one shape and with every corner identically arranged. The patterns formed by periodic tilings can be categorized into 17 wallpaper groups. A tiling that lacks a repeating pattern is called ""non-periodic"". An aperiodic tiling uses a small set of tile shapes that cannot form a repeating pattern. In the geometry of higher dimensions, a space-filling or honeycomb is also called a tessellation of space.A real physical tessellation is a tiling made of materials such as cemented ceramic squares or hexagons. Such tilings may be decorative patterns, or may have functions such as providing durable and water-resistant pavement, floor or wall coverings. Historically, tessellations were used in Ancient Rome and in Islamic art such as in the decorative tiling of the Alhambra palace. In the twentieth century, the work of M. C. Escher often made use of tessellations, both in ordinary Euclidean geometry and in hyperbolic geometry, for artistic effect. Tessellations are sometimes employed for decorative effect in quilting. Tessellations form a class of patterns in nature, for example in the arrays of hexagonal cells found in honeycombs.