Statement of Statement of Recent and Current Research (2007–2013)
... Control and inverse problems for partial differential equations on graphs. These problems belong to a rapidly developing interdisciplinary area of applied mathematics — analysis on (quantum) graphs. Differential equations on graphs are used to describe many physical processes such as mechanical vibr ...
... Control and inverse problems for partial differential equations on graphs. These problems belong to a rapidly developing interdisciplinary area of applied mathematics — analysis on (quantum) graphs. Differential equations on graphs are used to describe many physical processes such as mechanical vibr ...
A New Non-oscillatory Numerical Approach for Structural Dynamics
... R is the vector of the nodal load. Eq. (1) can be also obtained by the application of other discretization methods in space such as the finite difference method, the spectral element method, the boundary element method, the smoothed particle hydrodynamics (SPH) method and others. Many different nume ...
... R is the vector of the nodal load. Eq. (1) can be also obtained by the application of other discretization methods in space such as the finite difference method, the spectral element method, the boundary element method, the smoothed particle hydrodynamics (SPH) method and others. Many different nume ...
PDF (Chapter 1 - Initial-Value Problems for
... Table 1.1 shows the generated results. Notice that for N = 10 the differences between the analytical solution and the numerical approximation increase with x. In a problem where the analytical solution decreases with increasing values of the independent variable, a numerical method is unstable if th ...
... Table 1.1 shows the generated results. Notice that for N = 10 the differences between the analytical solution and the numerical approximation increase with x. In a problem where the analytical solution decreases with increasing values of the independent variable, a numerical method is unstable if th ...
Iso-P2 P1/P1/P1 Domain-Decomposition/Finite
... in various kinds of fields. In parallel computers of distributed memory type, data can be shared by communication procedures called message-passing, whose speed is slower than that of computations in a processor. From a practical point of view, it is important to reduce the amount of message-passing ...
... in various kinds of fields. In parallel computers of distributed memory type, data can be shared by communication procedures called message-passing, whose speed is slower than that of computations in a processor. From a practical point of view, it is important to reduce the amount of message-passing ...
Converting Mixed Numbers
... A “mixed number” is made up of a whole number and a fraction. An “improper fraction” is a fraction in which the numerator is greater than the denominator. ...
... A “mixed number” is made up of a whole number and a fraction. An “improper fraction” is a fraction in which the numerator is greater than the denominator. ...
direction field
... F(x, y) at several points (x, y), the result is called a direction field (or slope field). These line segments indicate the direction in which a solution curve is heading. So, the direction field helps us visualize the general shape of these curves. ...
... F(x, y) at several points (x, y), the result is called a direction field (or slope field). These line segments indicate the direction in which a solution curve is heading. So, the direction field helps us visualize the general shape of these curves. ...
Direct Least Square Fitting of Ellipses
... (from 2- to 2 ) for 100 runs and the distance between the true ellipse center and the center of the conic returned by the fitting algorithm was recorded. Returned hyperbolae were included for the other algorithms. Fig. 2a shows the 90th percentile error in the centers as a function of noise level. A ...
... (from 2- to 2 ) for 100 runs and the distance between the true ellipse center and the center of the conic returned by the fitting algorithm was recorded. Returned hyperbolae were included for the other algorithms. Fig. 2a shows the 90th percentile error in the centers as a function of noise level. A ...
COMBINED MEASUREMENT OF FLOW VELOCITY AND FILLING WITHIN
... measurements. With the LS method the only thing is to support the base with polynomials approximating the disturbances as stated in [5]. 3. PRACTICAL CONSTRAINTS Trying to obtain high accuracy of flow measurement with the above method, one can easily note some practical aspects that must certainly i ...
... measurements. With the LS method the only thing is to support the base with polynomials approximating the disturbances as stated in [5]. 3. PRACTICAL CONSTRAINTS Trying to obtain high accuracy of flow measurement with the above method, one can easily note some practical aspects that must certainly i ...
Section 3.9 - Differentials
... Since this is an implicit equation, you can either solve for y or use a method similar to the differentiation process in related rates/implicit differentiation. The following shows the latter: ...
... Since this is an implicit equation, you can either solve for y or use a method similar to the differentiation process in related rates/implicit differentiation. The following shows the latter: ...
Numerical integration
... There is no necessity to use equispaced points. By choosing the quadrature points xk appropriately we can derive n-points methods of order 2n + 1 (i.e. error varies as (b − a)2n+1 ), exact for polynomials of degree (2n − 1). These are called Gauss formulae and can give stunning accuracy. However, fo ...
... There is no necessity to use equispaced points. By choosing the quadrature points xk appropriately we can derive n-points methods of order 2n + 1 (i.e. error varies as (b − a)2n+1 ), exact for polynomials of degree (2n − 1). These are called Gauss formulae and can give stunning accuracy. However, fo ...
CS-184: Computer Graphics
... is a sum of a number of things Gravity: constant downward force proportional to mass ...
... is a sum of a number of things Gravity: constant downward force proportional to mass ...
1 Introduction 2 Errors in numerical solutions
... execute many tedious and repetitive calculations that produce accurate (even though not exact) solutions in a very short time. • For every type of mathematical problem there are several numerical techniques that can be used. The techniques differ in accuracy, length of calculations, and difficulty i ...
... execute many tedious and repetitive calculations that produce accurate (even though not exact) solutions in a very short time. • For every type of mathematical problem there are several numerical techniques that can be used. The techniques differ in accuracy, length of calculations, and difficulty i ...
Numerical Calculation of Certain Definite Integrals by Poisson`s
... present here a few of the simpler results. The purpose of this paper is to show that, by considering the method called the trapezoidal method (cf. Milne [1] p. 24) as a parabolic or quadratic function method, not only does one obtain a satisfying geometrical picture of an approximation curve in the ...
... present here a few of the simpler results. The purpose of this paper is to show that, by considering the method called the trapezoidal method (cf. Milne [1] p. 24) as a parabolic or quadratic function method, not only does one obtain a satisfying geometrical picture of an approximation curve in the ...
A MODIFIED TSVD METHOD FOR DISCRETE ILL
... xk of (1.1). Unfortunately, the matrix Ak generally is a poor approximation of A when k is small, which may lead to that xk is a poor approximation of x̂. It is the purpose of this paper to describe a modification of the TSVD method in which the matrix Ak is replaced by a matrix that is closer to A ...
... xk of (1.1). Unfortunately, the matrix Ak generally is a poor approximation of A when k is small, which may lead to that xk is a poor approximation of x̂. It is the purpose of this paper to describe a modification of the TSVD method in which the matrix Ak is replaced by a matrix that is closer to A ...
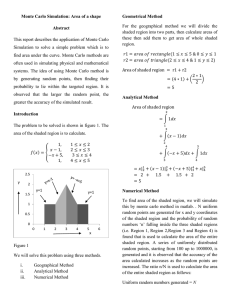
Monte Carlo Simulation: Area of a shape Abstract This report
... Simulation to solve a simple problem which is to find area under the curve. Monte Carlo methods are often used in simulating physical and mathematical systems. The idea of using Monte Carlo method is ...
... Simulation to solve a simple problem which is to find area under the curve. Monte Carlo methods are often used in simulating physical and mathematical systems. The idea of using Monte Carlo method is ...
Document
... Thus, to solve for the first time step, we substitute the initial conditions for the right-hand side and solve the 22 system of equations. The best way to do this is with LU decomposition since we will have to solve the system repeatedly. For the present case, because it’s easier to display, we wil ...
... Thus, to solve for the first time step, we substitute the initial conditions for the right-hand side and solve the 22 system of equations. The best way to do this is with LU decomposition since we will have to solve the system repeatedly. For the present case, because it’s easier to display, we wil ...
PowerPoint Presentation - Computer Science University of Victoria
... papers in hand, all excited: "I've just written an introduction to one of your papers. Read it so I can send it out right away for publication." For a minute I had no idea what he was talking about. To make a long story short, the problems on the blackboard which I had solved thinking they were home ...
... papers in hand, all excited: "I've just written an introduction to one of your papers. Read it so I can send it out right away for publication." For a minute I had no idea what he was talking about. To make a long story short, the problems on the blackboard which I had solved thinking they were home ...
Linear Programming for Optimization Mark A. Schulze, Ph.D
... programming problem of reasonable size in a reasonable amount of time. Only in the past ten years have other methods of solving linear programming problems (so-called interior point methods) developed to the point where they can be used to solve practical problems. ...
... programming problem of reasonable size in a reasonable amount of time. Only in the past ten years have other methods of solving linear programming problems (so-called interior point methods) developed to the point where they can be used to solve practical problems. ...
NUMERICAL OPTION PRICING IN THE PRESENCE OF BUBBLES
... as certain stochastic volatility models with a positive correlation between volatility and stock fluctuations, see [6]. The authors of [1] and [3] propose that a discounted underlying asset which is a strict local martingale (i.e. a local martingale but not a martingale) under the pricing measure can ...
... as certain stochastic volatility models with a positive correlation between volatility and stock fluctuations, see [6]. The authors of [1] and [3] propose that a discounted underlying asset which is a strict local martingale (i.e. a local martingale but not a martingale) under the pricing measure can ...