IOSR Journal of Mathematics (IOSR-JM) e-ISSN: 2278-5728.
... From above comparison table we have shown that Milne’s (modified) predictor-corrector formulae gives better accuracy and it also can minimize the calculating time as it takes less number of iterations. But, it is yet to implement proposed formulae to the real world problems. Though Milne’s (modified ...
... From above comparison table we have shown that Milne’s (modified) predictor-corrector formulae gives better accuracy and it also can minimize the calculating time as it takes less number of iterations. But, it is yet to implement proposed formulae to the real world problems. Though Milne’s (modified ...
T.Y.B.Sc. Mathematics - Veer Narmad South Gujarat University
... T.Y.B.Sc. Mathematics Paper - VIII (NUMERICAL ANALYSIS)* (Theory) To be in force from June 2009 [L : 3; P : 3] Unit 1: Errors in numerical calculations, Solution of Algebraic & Transcendental Equations : Numbers and their accuracy, Errors and their analysis, Absolute, Relative and Percentage errors, ...
... T.Y.B.Sc. Mathematics Paper - VIII (NUMERICAL ANALYSIS)* (Theory) To be in force from June 2009 [L : 3; P : 3] Unit 1: Errors in numerical calculations, Solution of Algebraic & Transcendental Equations : Numbers and their accuracy, Errors and their analysis, Absolute, Relative and Percentage errors, ...
Notes
... The formal name for this relationship is realization and the informal name is “implements” or “implements an interface” Inside the code, the class must create methods with the same signatures as those in the interface and give each method a method body. ...
... The formal name for this relationship is realization and the informal name is “implements” or “implements an interface” Inside the code, the class must create methods with the same signatures as those in the interface and give each method a method body. ...
Flux-based level set method on rectangular grids and computation
... Moreover, we always choose κ(0) = 1/2. where some external movement of the medium (water or air) changes our vision of the distance; see, e.g., the sailboat distance in [13, 14]. Here we prefer to extend the 2.2 Advection in normal direction notion of first arrival time function for this type of pro ...
... Moreover, we always choose κ(0) = 1/2. where some external movement of the medium (water or air) changes our vision of the distance; see, e.g., the sailboat distance in [13, 14]. Here we prefer to extend the 2.2 Advection in normal direction notion of first arrival time function for this type of pro ...
CURRICULUM PLAN
... Factorise quadratics (in order to find the intercepts) -students have already factorised quadratic expressions by decomposition and inspection but will need to learn the null factor theorem and the quadratic formula for finding the solutions to quadratic equations. ...
... Factorise quadratics (in order to find the intercepts) -students have already factorised quadratic expressions by decomposition and inspection but will need to learn the null factor theorem and the quadratic formula for finding the solutions to quadratic equations. ...
Style E 24 by 48
... of the multiple time-scales that coexist in the problem (whose equilibria arise through a complex balance of fluid-flow, magnetic-pull and diffusion effects) A change of unknown that enables evaluation of steady states in tissue and membrane layers through a highly accelerated time-stepping proced ...
... of the multiple time-scales that coexist in the problem (whose equilibria arise through a complex balance of fluid-flow, magnetic-pull and diffusion effects) A change of unknown that enables evaluation of steady states in tissue and membrane layers through a highly accelerated time-stepping proced ...
Java Programming class – Department of Network
... programming language. If a class is declared with no extends clause, then the compiler adds implicitly the code extend Object to the declaration for example Public class Employee { // code here ...
... programming language. If a class is declared with no extends clause, then the compiler adds implicitly the code extend Object to the declaration for example Public class Employee { // code here ...
Numerical Approximation of Forward
... analysed the roots of the characteristic equation of linear systems of MTFDE, which has led him to important results on the qualitative behaviour of their solutions. In particular, he has shown that a MTFDE may have a nonoscillatory solution in spite of the non-existence of real roots of its charact ...
... analysed the roots of the characteristic equation of linear systems of MTFDE, which has led him to important results on the qualitative behaviour of their solutions. In particular, he has shown that a MTFDE may have a nonoscillatory solution in spite of the non-existence of real roots of its charact ...
A Sample Abstract
... The probability of non-perforation is an important performance measure for armor effectiveness. To estimate this probability in homogeneous armor, live-fire testing of an anticipated threat ammunition into “infinitely”-thick armor may be conducted to record uncensored depths of penetration. Knowing ...
... The probability of non-perforation is an important performance measure for armor effectiveness. To estimate this probability in homogeneous armor, live-fire testing of an anticipated threat ammunition into “infinitely”-thick armor may be conducted to record uncensored depths of penetration. Knowing ...
The Method of Moments
... The method of moment (MoM) is a numerical procedure for solving linear operator equation by transforming it into a system of simultaneous linear algebraic equation, referred to as matrix equation. Many problems in electromagnetics can be cast in the form of integral equations. An integral equation i ...
... The method of moment (MoM) is a numerical procedure for solving linear operator equation by transforming it into a system of simultaneous linear algebraic equation, referred to as matrix equation. Many problems in electromagnetics can be cast in the form of integral equations. An integral equation i ...
A new CFD framework for transport equations: ENATE scheme for
... 1st and 2nd order schemes are widespread in CFD. For many industrial applications they are good enough, but in those where the accuracy is a key-factor, a discretization with higher accuracy than 2nd or 3rd order is required. A high-order approximation using few grid-nodes is the aim of ENATE scheme ...
... 1st and 2nd order schemes are widespread in CFD. For many industrial applications they are good enough, but in those where the accuracy is a key-factor, a discretization with higher accuracy than 2nd or 3rd order is required. A high-order approximation using few grid-nodes is the aim of ENATE scheme ...
Technical Article Recent Developments in Discontinuous Galerkin Methods for the Time–
... have been proved and numerically validated in [14] for Method I, and in [15] for Method II. Theorem 2: Assume that the analytical solution (u, p) of (10) satisfies the smoothness assumptions u ∈ H s (Th )3 , ∇ × u ∈ H s (Th )3 and p ∈ H s+1 (Th ), for s > 1/2, and let (uh , ph ) be the DG approximat ...
... have been proved and numerically validated in [14] for Method I, and in [15] for Method II. Theorem 2: Assume that the analytical solution (u, p) of (10) satisfies the smoothness assumptions u ∈ H s (Th )3 , ∇ × u ∈ H s (Th )3 and p ∈ H s+1 (Th ), for s > 1/2, and let (uh , ph ) be the DG approximat ...
Robust and scalable multiphysics solvers for unfitted finite element
... pipeline, since mesh generators do not usually scale properly. In some other situations, like in additive manufacturing simulations, the geometry evolves in time, and the use of boddy-fitted meshes is not suitable. On the contrary, algorithms to create adaptive cartesian meshes are highly scalable. ...
... pipeline, since mesh generators do not usually scale properly. In some other situations, like in additive manufacturing simulations, the geometry evolves in time, and the use of boddy-fitted meshes is not suitable. On the contrary, algorithms to create adaptive cartesian meshes are highly scalable. ...
Numerical Solutions of Differential Equations
... The way we will “solve” a differential equation is to use the definition of a function. That is to say if we are given a differential equation y’(x) = f(x,y) with a boundary condition y(x0) = y0 and another value of x, say xact we can find a number yact so that y(xact) = yact. The problem that exist ...
... The way we will “solve” a differential equation is to use the definition of a function. That is to say if we are given a differential equation y’(x) = f(x,y) with a boundary condition y(x0) = y0 and another value of x, say xact we can find a number yact so that y(xact) = yact. The problem that exist ...
MATHS – Calculations policy - Binfield Church of England Primary
... Children should also know that 3 x 5 has the same answer as 5 x 3. This can also be shown on the number line. ...
... Children should also know that 3 x 5 has the same answer as 5 x 3. This can also be shown on the number line. ...
Document
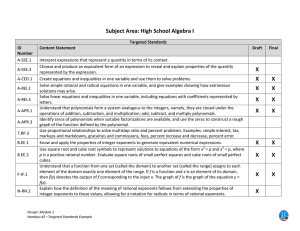
... Create equations and inequalities in one variable and use them to solve problems. Solve simple rational and radical equations in one variable, and give examples showing how extraneous solutions may arise. Solve linear equations and inequalities in one variable, including equations with coefficients ...
... Create equations and inequalities in one variable and use them to solve problems. Solve simple rational and radical equations in one variable, and give examples showing how extraneous solutions may arise. Solve linear equations and inequalities in one variable, including equations with coefficients ...
1 Review of Least Squares Solutions to Overdetermined Systems
... any solution to (3) is a correct solution to our problem. In this case, there will be infinitely many solutions, and all of them are correct solutions to the least squares problem. (In general, if a matrix C is singular then the system Cx = y may not have any solution. However, due to the structure ...
... any solution to (3) is a correct solution to our problem. In this case, there will be infinitely many solutions, and all of them are correct solutions to the least squares problem. (In general, if a matrix C is singular then the system Cx = y may not have any solution. However, due to the structure ...
linear-system
... While conditions for convergence of this method are readily established, useful theoretical estimates of the rate of convergence of the Kaczmarz method (or more generally of the alternating projection method for linear subspaces) are difficult to obtain, at least for m > 2. Known estimates for the r ...
... While conditions for convergence of this method are readily established, useful theoretical estimates of the rate of convergence of the Kaczmarz method (or more generally of the alternating projection method for linear subspaces) are difficult to obtain, at least for m > 2. Known estimates for the r ...
1 Numerical Solution to Quadratic Equations 2 Finding Square
... numbers are actually good, accepatable approximations of the true π, b. Now, we want to compute π − b, and want to have a similarly good approximate representation: 10-11 significant digits, i.e., once the zeros end and the number begins. However, all we can do is subtract the given approximation to ...
... numbers are actually good, accepatable approximations of the true π, b. Now, we want to compute π − b, and want to have a similarly good approximate representation: 10-11 significant digits, i.e., once the zeros end and the number begins. However, all we can do is subtract the given approximation to ...
A class of Methods Based on Cubic Non
... In this paper, we are concerned with the problem of applying cubic parametric spline functions to develop a numerical method for obtaining approximation for the solution for the linear time fractional diffusion equation. The special parametric spline used in this paper is in fact trigonometric-polyn ...
... In this paper, we are concerned with the problem of applying cubic parametric spline functions to develop a numerical method for obtaining approximation for the solution for the linear time fractional diffusion equation. The special parametric spline used in this paper is in fact trigonometric-polyn ...
Brief Explanation of Integration Schemes
... scheme. It allows for the calculation of xn+1 in terms of xn in a straightforward manner at each time step, but is sensitive to stability issues (like all explicit methods) which will be discussed next. ...
... scheme. It allows for the calculation of xn+1 in terms of xn in a straightforward manner at each time step, but is sensitive to stability issues (like all explicit methods) which will be discussed next. ...