Research on Mathematical Models of Tax Planning for
... depreciation are certainly not determinate, so the risk element should be considered undoubtedly. Berg & Moore[12] consider the uncertainty of future cash flows from operation in comparing the accelerated depreciation method and the straight-line depreciation method, derive for the depreciation meth ...
... depreciation are certainly not determinate, so the risk element should be considered undoubtedly. Berg & Moore[12] consider the uncertainty of future cash flows from operation in comparing the accelerated depreciation method and the straight-line depreciation method, derive for the depreciation meth ...
Numerical methods for physics simulations.
... α = 1/2 is best as it corresponds to the midpont rule but one must explictly add some damping. The matrix multiplying xn+1 is symmetric but not necessarily positive definite. In addition, the factor of k is problematic as the problem is ill-posed when this gets too large. Matrix K contains second de ...
... α = 1/2 is best as it corresponds to the midpont rule but one must explictly add some damping. The matrix multiplying xn+1 is symmetric but not necessarily positive definite. In addition, the factor of k is problematic as the problem is ill-posed when this gets too large. Matrix K contains second de ...
PLATFORM FOR BUILDING PDE-BASED PROBLEM
... • A processing class expects certain input from the descriptive objects on the argument list • A processing class has its application range • Java interface can be used as a reference data type – Only an instance of a class that implements the interface can be assigned to a reference variable whose ...
... • A processing class expects certain input from the descriptive objects on the argument list • A processing class has its application range • Java interface can be used as a reference data type – Only an instance of a class that implements the interface can be assigned to a reference variable whose ...
Solutions for the exercises - Delft Center for Systems and Control
... Figure 3: Feasible set and contour plot for Exercise 2.1 Solution: Figure 3 shows the contour plot and the feasible region of the optimization problem. The solution is in a vertex of the feasible set, which is obtained with the graphical method (we shift one of the contour lines in a parallel way in ...
... Figure 3: Feasible set and contour plot for Exercise 2.1 Solution: Figure 3 shows the contour plot and the feasible region of the optimization problem. The solution is in a vertex of the feasible set, which is obtained with the graphical method (we shift one of the contour lines in a parallel way in ...
Discrete (Difference) Equations
... and the equation has two fixed points at yn = 0 and 1. That these solutions are fixed points is easy to verify on substitution into equation (11).3 The fixed points of a difference equation are rather special because if any sequence ever “visits” one of the fixed points, it will always remain there ...
... and the equation has two fixed points at yn = 0 and 1. That these solutions are fixed points is easy to verify on substitution into equation (11).3 The fixed points of a difference equation are rather special because if any sequence ever “visits” one of the fixed points, it will always remain there ...
Linear Angle Based Parameterization - HAL
... We experimented the method with a large number of complicated test cases, including surfaces with high curvature (see Figure 3), and the example known to make linear conformal parameterization methods fail (’obtuse’ entry in Table 1 and Figure 4). Although this is not guaranteed, for all these test ...
... We experimented the method with a large number of complicated test cases, including surfaces with high curvature (see Figure 3), and the example known to make linear conformal parameterization methods fail (’obtuse’ entry in Table 1 and Figure 4). Although this is not guaranteed, for all these test ...
Developing And Comparing Numerical Methods For Computing The Inverse Fourier Transform Abstract
... these parameters is the total number of samples taken in the frequency domain ( N ). This parameter is used in all the methods. The reconstruction of the function will have to be limited to a finite interval [ T , 0] , for some positive number T . Also, the distance between samples reconstructed in ...
... these parameters is the total number of samples taken in the frequency domain ( N ). This parameter is used in all the methods. The reconstruction of the function will have to be limited to a finite interval [ T , 0] , for some positive number T . Also, the distance between samples reconstructed in ...
Connections Between Duality in Control Theory and Convex
... problem from control theory proceeds as follows: The control problem is reformulated (or in many cases, approximately reformulated) as a convex optimization problem, which is then solved using convex programming methods. Once the control problem is reformulated into a convex optimization problem, th ...
... problem from control theory proceeds as follows: The control problem is reformulated (or in many cases, approximately reformulated) as a convex optimization problem, which is then solved using convex programming methods. Once the control problem is reformulated into a convex optimization problem, th ...
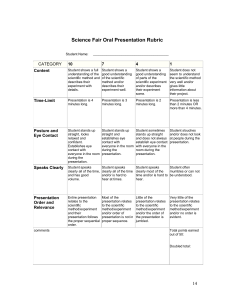
Oral Presentation Rubric : Science Fair Presentation
... Little of the presentation relates to the scientific method/experiment and/or the order of the presentation is ...
... Little of the presentation relates to the scientific method/experiment and/or the order of the presentation is ...
Parallel Solution of the Poisson Problem Using
... • Relaxation methods (which are related) are usually better, but can be less reliable. ...
... • Relaxation methods (which are related) are usually better, but can be less reliable. ...
A finite element method for transient compressible flow in pipelines
... This method was used without any stability problems. The resulting non-linear system was solved by the Newton-Raphson method. In each iteration it is necessary to solve a set of linear equations. The matrix is sparse with a bandwidth of ten. A standard subroutine for profile equation-solving, called ...
... This method was used without any stability problems. The resulting non-linear system was solved by the Newton-Raphson method. In each iteration it is necessary to solve a set of linear equations. The matrix is sparse with a bandwidth of ten. A standard subroutine for profile equation-solving, called ...
Exceptions
... the problem. Such methods are called exception handlers. An exception handler can either correct the problem (fault handlers), gracefully terminate the program (trap handlers), or simply ignore the problem. Java recognizes two types of problems: errors and exceptions. Exceptions can be further divid ...
... the problem. Such methods are called exception handlers. An exception handler can either correct the problem (fault handlers), gracefully terminate the program (trap handlers), or simply ignore the problem. Java recognizes two types of problems: errors and exceptions. Exceptions can be further divid ...
Root Finding
... A root x∗ is simple if f (x∗ ) = 0, if the function f " exists everywhere on an open interval containing x∗ , and if f " (x∗ ) "= 0. So, x∗ = 0 is a simple root of f (x) = x and f (x) = ln (x + 1) (choose the open interval to be (− 21 , 12 )). But, x∗ = 0 is not√a simple root of f (x) = xn , n > 1 b ...
... A root x∗ is simple if f (x∗ ) = 0, if the function f " exists everywhere on an open interval containing x∗ , and if f " (x∗ ) "= 0. So, x∗ = 0 is a simple root of f (x) = x and f (x) = ln (x + 1) (choose the open interval to be (− 21 , 12 )). But, x∗ = 0 is not√a simple root of f (x) = xn , n > 1 b ...
DIVERGENCE-FREE WAVELET PROJECTION METHOD
... or wavelet method [5, 18], equation (3.3) has the advantage of reducing the number of degree of freedom: only coefficients {dj,k } are computed instead of one type of coefficients per components of the velocity v. Moreover, adaptive methods can be applied and optimal preconditioning for the stiffnes ...
... or wavelet method [5, 18], equation (3.3) has the advantage of reducing the number of degree of freedom: only coefficients {dj,k } are computed instead of one type of coefficients per components of the velocity v. Moreover, adaptive methods can be applied and optimal preconditioning for the stiffnes ...
A Spring-Embedding Approach for the Facility Layout Problem
... for small or greatly restricted problems. 3 For this reason, most of the solution methodologies in the literature are based on heuristics. In general, the facility layout problems found in the literature deal with the arrangement of rectangular departments. There are applications, however, in which ...
... for small or greatly restricted problems. 3 For this reason, most of the solution methodologies in the literature are based on heuristics. In general, the facility layout problems found in the literature deal with the arrangement of rectangular departments. There are applications, however, in which ...
Chapter 4 Methods
... public static int sign(int n) { if (n > 0) return 1; else if (n == 0) return 0; else if (n < 0) return –1; ...
... public static int sign(int n) { if (n > 0) return 1; else if (n == 0) return 0; else if (n < 0) return –1; ...
Quantifier-Free Linear Arithmetic
... 4. Calculate the new values for the others rows. New row numbers = numbers in old row - ( Number in old row above or below pivot number * Corresponding number in the new row) 5. Calculate the Cj and the Cj – Zj values for this tableau. If there are any Cj – Zj numbers greater than zero, return to st ...
... 4. Calculate the new values for the others rows. New row numbers = numbers in old row - ( Number in old row above or below pivot number * Corresponding number in the new row) 5. Calculate the Cj and the Cj – Zj values for this tableau. If there are any Cj – Zj numbers greater than zero, return to st ...