Unconstrained Nonlinear Optimization, Constrained Nonlinear
... can be any solution to Ax = b F spans the nullspace of A A way to find an F: compute SVD of A, A = U S V’, for A having k nonzero singular values, set F = U(:, k+1:end) n ...
... can be any solution to Ax = b F spans the nullspace of A A way to find an F: compute SVD of A, A = U S V’, for A having k nonzero singular values, set F = U(:, k+1:end) n ...
Chapter 1 Finite Difference Solution of Linear Second Order Elliptic
... As we discussed in the previous sections the finite difference solution of elliptic equations results in systems of linear algebraic equations. In one dimension with uniform step-size, the matrix Ah is a uniformly tridiagonal sparse symmetric matrix, while in two-dimension, albeit Ah is symmetric, t ...
... As we discussed in the previous sections the finite difference solution of elliptic equations results in systems of linear algebraic equations. In one dimension with uniform step-size, the matrix Ah is a uniformly tridiagonal sparse symmetric matrix, while in two-dimension, albeit Ah is symmetric, t ...
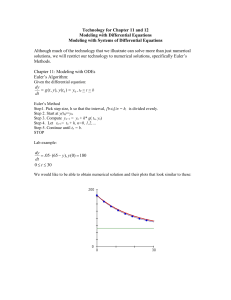
Technology for Chapter 11 and 12
... Step 2. Start at y(t0)=y0. Step 3. Compute yn+1 = yn + h* g( tn, yn) Step 4. Let tn+1= tn + h, n=0, 1,2,… Step 5. Continue until tn = b. STOP Lab example: ...
... Step 2. Start at y(t0)=y0. Step 3. Compute yn+1 = yn + h* g( tn, yn) Step 4. Let tn+1= tn + h, n=0, 1,2,… Step 5. Continue until tn = b. STOP Lab example: ...
Numerical Study on ESR of Nanomagnet V and Dzyaloshinsky-Moriya In- teraction
... Department of Physics, Graduate School of Science, The University of Tokyo, Hongo, Tokyo 113-0033, Japan ...
... Department of Physics, Graduate School of Science, The University of Tokyo, Hongo, Tokyo 113-0033, Japan ...
Minimum Weighted Residual Methods in Endogenous - cerge-ei
... Solving these models via derivation of the first order necessary conditions by means of the Pontryagin Maximum Principle or the Bellman dynamical programming approach, we face the so called two point boundary value (TPBV) problem which is much more difficult to solve than the Cauchy initial value (C ...
... Solving these models via derivation of the first order necessary conditions by means of the Pontryagin Maximum Principle or the Bellman dynamical programming approach, we face the so called two point boundary value (TPBV) problem which is much more difficult to solve than the Cauchy initial value (C ...
Solve simultaneous linear equations by the elimination method
... Note: In the process of solving simultaneous linear equations, either one of the unknowns may be eliminated first ...
... Note: In the process of solving simultaneous linear equations, either one of the unknowns may be eliminated first ...
Chapter 4 Methods
... Pass by value: the parameter is allocated the required memory storage and the value of the argument is copied to the parameter. There are 2 separate copies of the same values. Example 4.2 Testing Pass by value This program demonstrates passing values to the methods. TestPassByValue ...
... Pass by value: the parameter is allocated the required memory storage and the value of the argument is copied to the parameter. There are 2 separate copies of the same values. Example 4.2 Testing Pass by value This program demonstrates passing values to the methods. TestPassByValue ...
Methods
... When a method is called, the statements inside the corresponding method are executed When all statements in the method has been executed, the execution will resume at the program location of the method call ...
... When a method is called, the statements inside the corresponding method are executed When all statements in the method has been executed, the execution will resume at the program location of the method call ...
The Fundamental Theorem of Numerical Analysis
... A problem consists of data and an equation that must we say the problem is well-posed. In particular, an initial be solved for an unknown. An initial value problem value problem is well-posed (over a finite time interval) if (IVP) consists of initial data (and possibly boundary data) the factor by w ...
... A problem consists of data and an equation that must we say the problem is well-posed. In particular, an initial be solved for an unknown. An initial value problem value problem is well-posed (over a finite time interval) if (IVP) consists of initial data (and possibly boundary data) the factor by w ...
Advanced Object Oriented Systems
... • A method is said to be maximally specific for a method invocation if it is applicable and accessible and there is no other applicable and accessible method that is more specific. • If there is only one maximally specific method for a given method invocation, it is called the most specific method • ...
... • A method is said to be maximally specific for a method invocation if it is applicable and accessible and there is no other applicable and accessible method that is more specific. • If there is only one maximally specific method for a given method invocation, it is called the most specific method • ...
Advanced Numerical Methods - Université catholique de Louvain
... -To select and to apply the right method for a given problem. -To evaluate the algorithmic complexity of a method. -To efficiently use the numerical available libraries (Lapack) -To provide an estimate of the error. -To evaluate the quality of a mesh for a given method. -To perform a calculation on ...
... -To select and to apply the right method for a given problem. -To evaluate the algorithmic complexity of a method. -To efficiently use the numerical available libraries (Lapack) -To provide an estimate of the error. -To evaluate the quality of a mesh for a given method. -To perform a calculation on ...
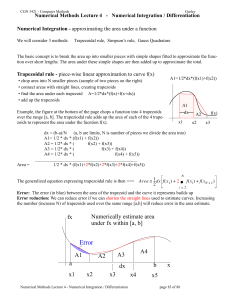
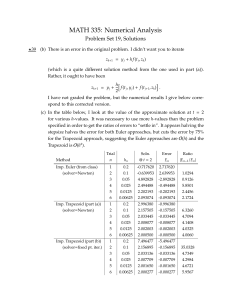
NM_lect_4 - essie-uf
... The error using trapezoidal rule comes from using a series of straight lines to represent a curve. To reduce this error, we’ll now look at using a series of second order curves to represt the function. ...
... The error using trapezoidal rule comes from using a series of straight lines to represent a curve. To reduce this error, we’ll now look at using a series of second order curves to represt the function. ...
solving rational inequalities
... 1. If needed, rewrite the inequality so that 0 is on one side. This usually requires you to add or subtract term(s) to both sides of the inequality. 2. If needed, simplify the non-zero side so that there is a single fraction. This usually requires finding a common denominator. 3. Set the numerator e ...
... 1. If needed, rewrite the inequality so that 0 is on one side. This usually requires you to add or subtract term(s) to both sides of the inequality. 2. If needed, simplify the non-zero side so that there is a single fraction. This usually requires finding a common denominator. 3. Set the numerator e ...
Practice Problems
... 1.[14] Circle the letter corresponding to the differential equation whose direction field is given in the figure below. Then explain your reasons for your answer. Note that “My calculator says so.” is not a valid reason. (a) y′ = y + 1 ...
... 1.[14] Circle the letter corresponding to the differential equation whose direction field is given in the figure below. Then explain your reasons for your answer. Note that “My calculator says so.” is not a valid reason. (a) y′ = y + 1 ...
Estimating Passenger Demands from Truncated Samples
... degree of correlation (R=. 63), whereas the ones for the standard deviation are only loosely correlated (R=.19) . ...
... degree of correlation (R=. 63), whereas the ones for the standard deviation are only loosely correlated (R=.19) . ...
The Method of Vieta
... The method of Vieta Jumping can be very useful if from the divisibility of some positive integers, some properties of their quotient are asked to be infered. The idea is to assume the existence of a solution for which the statement in question is wrong and then to consider the given relation as a qu ...
... The method of Vieta Jumping can be very useful if from the divisibility of some positive integers, some properties of their quotient are asked to be infered. The idea is to assume the existence of a solution for which the statement in question is wrong and then to consider the given relation as a qu ...
Comments on the “Three Piles” Problem
... Solved 10000 problems of size 5 in 15 milliseconds. Average time per problem: 0.0015 ms. Solved 200 problems of size 10 in 16 milliseconds. Average time per problem: 0.08 ms. Solved 200 problems of size 15 in 718 milliseconds. Average time per problem: 3.59 ms. Solved 200 problems of size 20 in 3471 ...
... Solved 10000 problems of size 5 in 15 milliseconds. Average time per problem: 0.0015 ms. Solved 200 problems of size 10 in 16 milliseconds. Average time per problem: 0.08 ms. Solved 200 problems of size 15 in 718 milliseconds. Average time per problem: 3.59 ms. Solved 200 problems of size 20 in 3471 ...
1 Time-Integrators
... Remark 1 The leapfrog method is perhaps the most common explicit Eulerian method found in geophysical fluid dynamics because it is a symplectic method, that is, a method which preserves all Lagrangian invariants. For hyperbolic equations the ideal method is one which has no numerical diffusion (dam ...
... Remark 1 The leapfrog method is perhaps the most common explicit Eulerian method found in geophysical fluid dynamics because it is a symplectic method, that is, a method which preserves all Lagrangian invariants. For hyperbolic equations the ideal method is one which has no numerical diffusion (dam ...