Honors Geometry Name_______________________________
... a) The diagonals of a parallelogram bisect the angles of the parallelogram. b) The diagonals of a rhombus are perpendicular bisectors of each other. c) The diagonals of an isosceles trapezoid are congruent. d) One diagonal of a kite bisects the other diagonal. e) The diagonals of a rectangle are con ...
... a) The diagonals of a parallelogram bisect the angles of the parallelogram. b) The diagonals of a rhombus are perpendicular bisectors of each other. c) The diagonals of an isosceles trapezoid are congruent. d) One diagonal of a kite bisects the other diagonal. e) The diagonals of a rectangle are con ...
Full text
... F2m+2 ~~ 1 contains respectively (on the basis of the inductive assumptions) m and m + 7 terms. If to these decompositions we add on the left-hand side the term F2m+3 we obtain the correct decomposition of numbers F 2m+4 ~ 2 and F2m+4 ~ ?• These latter contain respectively m + 1 and m + 2 terms. Fro ...
... F2m+2 ~~ 1 contains respectively (on the basis of the inductive assumptions) m and m + 7 terms. If to these decompositions we add on the left-hand side the term F2m+3 we obtain the correct decomposition of numbers F 2m+4 ~ 2 and F2m+4 ~ ?• These latter contain respectively m + 1 and m + 2 terms. Fro ...
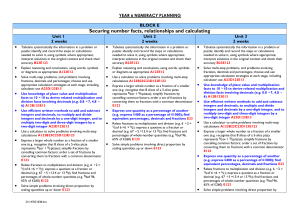
y6 block e plan - School
... decimal places, to multiply HTU U and TU TU, and to divide TU U find equivalent fractions understand percentage as the number of parts in every 100, and express tenths and hundredths as percentages use sequences to scale numbers up or down find simple fractions of percentages of quantities ...
... decimal places, to multiply HTU U and TU TU, and to divide TU U find equivalent fractions understand percentage as the number of parts in every 100, and express tenths and hundredths as percentages use sequences to scale numbers up or down find simple fractions of percentages of quantities ...
CMP3 Glossary - Connected Mathematics Project
... basic design element A part of a pattern or design that, when transformed using at least one type of symmetry transformation, will produce the entire design. benchmark A reference number that can be used to estimate the size of other numbers. For work with fractions, 0, 1/2, and 1 are good benchmark ...
... basic design element A part of a pattern or design that, when transformed using at least one type of symmetry transformation, will produce the entire design. benchmark A reference number that can be used to estimate the size of other numbers. For work with fractions, 0, 1/2, and 1 are good benchmark ...
Logs and significant figures
... When taking an antilog, count the digits in the matissa – that’s the number of significant figures your answer should have. ...
... When taking an antilog, count the digits in the matissa – that’s the number of significant figures your answer should have. ...