Chapter_007-ppt-Intro-to-Cl-Phar-6th-ed
... Elsevier items and derived items © 2010, 2006, 2003, 2000 by Mosby, an imprint of Elsevier Inc. ...
... Elsevier items and derived items © 2010, 2006, 2003, 2000 by Mosby, an imprint of Elsevier Inc. ...
7-3 - TeacherWeb
... 7-3 Multiplication Properties of Exponents Products of powers with the same base can be found by writing each power as a repeated multiplication. ...
... 7-3 Multiplication Properties of Exponents Products of powers with the same base can be found by writing each power as a repeated multiplication. ...
What every computer scientist should know about floating
... The IEEE standard goes further than just requiring the use of a guard digit. It gives an algorithm for addition, subtraction, multiplication, division, and square root and requires that implementations produce the same result as that algorithm. Thus, when a program is moved from one machine to anoth ...
... The IEEE standard goes further than just requiring the use of a guard digit. It gives an algorithm for addition, subtraction, multiplication, division, and square root and requires that implementations produce the same result as that algorithm. Thus, when a program is moved from one machine to anoth ...
What every computer scientist should know about floating
... The IEEE standard goes further than just requiring the use of a guard digit. It gives an algorithm for addition, subtraction, multiplication, division, and square root and requires that implementations produce the same result as that algorithm. Thus, when a program is moved from one machine to anoth ...
... The IEEE standard goes further than just requiring the use of a guard digit. It gives an algorithm for addition, subtraction, multiplication, division, and square root and requires that implementations produce the same result as that algorithm. Thus, when a program is moved from one machine to anoth ...
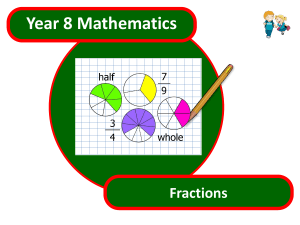
FRACTIONS, GCF,REDUCING
... 1. The numerator of the fraction is 1. 2. The numerator and denominator are consecutive(1 apart)! 3. The numerator and denominator are prime numbers. 4. The numerator is a prime number and it does not divide into the denominator evenly. ...
... 1. The numerator of the fraction is 1. 2. The numerator and denominator are consecutive(1 apart)! 3. The numerator and denominator are prime numbers. 4. The numerator is a prime number and it does not divide into the denominator evenly. ...