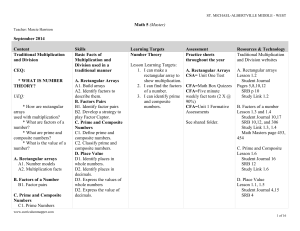
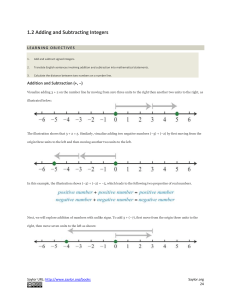
Complex Numbers - BCI
... Up until now you have been unable to find the square root of a negative number. In more advance mathematics you can take the square root of a negative number and you get a new type of number, that is a Complex Number. Complex numbers were first invented / discovered by an Italian mathematician Gerol ...
... Up until now you have been unable to find the square root of a negative number. In more advance mathematics you can take the square root of a negative number and you get a new type of number, that is a Complex Number. Complex numbers were first invented / discovered by an Italian mathematician Gerol ...
Loops - Telerik
... repeating execution of a block of statements May execute a code block fixed number of times May execute a code block while given condition ...
... repeating execution of a block of statements May execute a code block fixed number of times May execute a code block while given condition ...
Midterm 1
... 6. Write code to implement the following flow chart. The user will enter 10 numbers between 0 and 100 and the program will count how many are 90, how many are in the interval [80, 90) and how many are less than 80 and then report the results. ...
... 6. Write code to implement the following flow chart. The user will enter 10 numbers between 0 and 100 and the program will count how many are 90, how many are in the interval [80, 90) and how many are less than 80 and then report the results. ...