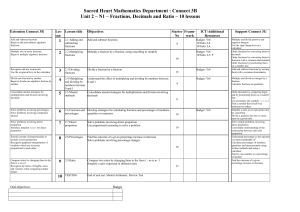
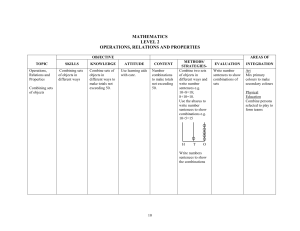
No Slide Title
... be true. A conjecture is based on reasoning and may be true or false. A counterexample is an example that disproves a conjecture, or shows that it is false. One counterexample is enough to disprove a conjecture. ...
... be true. A conjecture is based on reasoning and may be true or false. A counterexample is an example that disproves a conjecture, or shows that it is false. One counterexample is enough to disprove a conjecture. ...
Forty Second Annual Columbus State University Invitational
... Sponsored by The Columbus State University Department of Mathematics March 5, 2016 ...
... Sponsored by The Columbus State University Department of Mathematics March 5, 2016 ...
Numeracy Overview Year 2 - St Marys Primary School, Killyclogher
... combining sets to find ‘how many’ Match objects in real contexts, knife to fork Demonstrate understanding that when adding, answer will be larger. Count in 1’s and 2’s forwards/backwards from zero, within 10 then 20 , 10’s – break or pause at 10 Recognise, read, write numbers to 10 Know number befor ...
... combining sets to find ‘how many’ Match objects in real contexts, knife to fork Demonstrate understanding that when adding, answer will be larger. Count in 1’s and 2’s forwards/backwards from zero, within 10 then 20 , 10’s – break or pause at 10 Recognise, read, write numbers to 10 Know number befor ...