Integers
... A balloon floated at a height of 48 feet. Which number is most closely represented Which point on the number line is the by Point T on the number line? closest to 48? ...
... A balloon floated at a height of 48 feet. Which number is most closely represented Which point on the number line is the by Point T on the number line? closest to 48? ...
NOTICE from J - JamesGoulding.com
... then you can skip the next few paragraphs. If not, read it carefully. Complex numbers were introduced to answer the question of "What is the solution to x^2 + 1 = 0 (x squared plus 1 equals 0)?" Now, you'd think that such an equation would have no solution, and this is true if x has to be a *real* n ...
... then you can skip the next few paragraphs. If not, read it carefully. Complex numbers were introduced to answer the question of "What is the solution to x^2 + 1 = 0 (x squared plus 1 equals 0)?" Now, you'd think that such an equation would have no solution, and this is true if x has to be a *real* n ...
Chapter 1
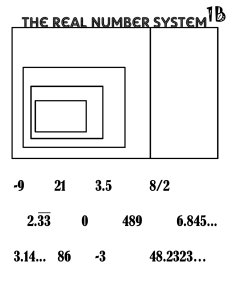
... 5.1.1.9. simplest form – when all common factors from the numerator and denominator have been removed; we say that the numerator and the denominator are relatively prime when a fraction is in simplest form 5.1.1.10. lowest terms – same as simplest form 5.1.1.11. denseness – there are no holes in the ...
... 5.1.1.9. simplest form – when all common factors from the numerator and denominator have been removed; we say that the numerator and the denominator are relatively prime when a fraction is in simplest form 5.1.1.10. lowest terms – same as simplest form 5.1.1.11. denseness – there are no holes in the ...
Quaternions are turning tomb raiders on their heads
... where the cube roots must be chosen so that their product is p3 . The problem arises in that, even if the cubic equation has three real roots, the term under the square root may be negative. However, Cardano’s formula does give all three real solutions provided you are happy manipulating square root ...
... where the cube roots must be chosen so that their product is p3 . The problem arises in that, even if the cubic equation has three real roots, the term under the square root may be negative. However, Cardano’s formula does give all three real solutions provided you are happy manipulating square root ...
Radicals and Complex Numbers Louisiana
... Rules for Simplifying n b identify and give examples of the rules for even and odd values of n. Product and Quotient Rules for Radicals – identify and give examples of the rules. Rationalizing the Denominator – explain: what does it mean and why do it – the process for rationalizing a denominator ...
... Rules for Simplifying n b identify and give examples of the rules for even and odd values of n. Product and Quotient Rules for Radicals – identify and give examples of the rules. Rationalizing the Denominator – explain: what does it mean and why do it – the process for rationalizing a denominator ...
unit 1 vocabulary: real numbers - angel
... Standard form is a way of writing down very large or very small numbers easily. For example, 10³ = 1000, so 4 × 10³ = 4000. So 4000 can be written as 4 × 10³. This idea can be used to write even larger numbers down easily in standard form. Small numbers can also be written in standard form. However, ...
... Standard form is a way of writing down very large or very small numbers easily. For example, 10³ = 1000, so 4 × 10³ = 4000. So 4000 can be written as 4 × 10³. This idea can be used to write even larger numbers down easily in standard form. Small numbers can also be written in standard form. However, ...