Document
... • Church and Turing independently showed that there is no general decision procedure to check the validity of formulas of the first order logic. ...
... • Church and Turing independently showed that there is no general decision procedure to check the validity of formulas of the first order logic. ...
On Cantor`s First Uncountability Proof, Pick`s Theorem
... We consider only the case a1 > a2 ; the proof in the case a2 > a1 is very similar. Since a1 > a2 , we get that (bn ) is a strictly decreasing sequence, while (cn ) is strictly increasing. Moreover, every cn is less than every bm . Furthermore, note that if bn = ak and bn+1 = a` , then k < `; a simil ...
... We consider only the case a1 > a2 ; the proof in the case a2 > a1 is very similar. Since a1 > a2 , we get that (bn ) is a strictly decreasing sequence, while (cn ) is strictly increasing. Moreover, every cn is less than every bm . Furthermore, note that if bn = ak and bn+1 = a` , then k < `; a simil ...
Exponential Sums and Diophantine Problems
... and minor “arcs,” with the major arcs consisting of points that are well-approximated by a rational number with small denominator. We should remark that the term “arcs” persists as a result of Hardy and Littlewood’s original approach to the problem, in which they used Cauchy’s integral formula to re ...
... and minor “arcs,” with the major arcs consisting of points that are well-approximated by a rational number with small denominator. We should remark that the term “arcs” persists as a result of Hardy and Littlewood’s original approach to the problem, in which they used Cauchy’s integral formula to re ...
Intuitionistic completeness part I
... Intuitionistic first-order logic, iFOL The BHK semantics for iFOL is the intended semantics, faithful to the intuitionistic conception of knowledge. In contrast to the classical situation, there has been no intuitionistic completeness proof with respect to the intended semantics. To explain this con ...
... Intuitionistic first-order logic, iFOL The BHK semantics for iFOL is the intended semantics, faithful to the intuitionistic conception of knowledge. In contrast to the classical situation, there has been no intuitionistic completeness proof with respect to the intended semantics. To explain this con ...
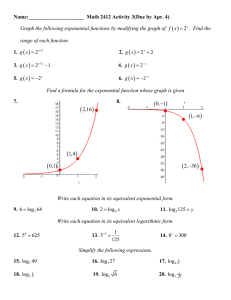
Name: Math 2412 Activity 3(Due by Apr. 4) Graph the following
... 116. A sequence an is given recursively by an1 2an n2 . If a4 23 , then what’s a1 ? 117. Find x so that x 3,2x 1,5x 2 are consecutive terms of an arithmetic sequence. 118. Find x so that 2x,3x 2,5x 3 are consecutive terms of an arithmetic sequence. 119. How many terms must be add ...
... 116. A sequence an is given recursively by an1 2an n2 . If a4 23 , then what’s a1 ? 117. Find x so that x 3,2x 1,5x 2 are consecutive terms of an arithmetic sequence. 118. Find x so that 2x,3x 2,5x 3 are consecutive terms of an arithmetic sequence. 119. How many terms must be add ...
Refinement Modal Logic
... the agent’s accessibility relation. In [55] the future event logic is introduced. It augments the multi-agent logic of knowledge with an operation ∀ϕ that stands for “ϕ holds after all informative events” — the diamond version ∃ϕ stands for “there is an informative event after which ϕ.” The proposal ...
... the agent’s accessibility relation. In [55] the future event logic is introduced. It augments the multi-agent logic of knowledge with an operation ∀ϕ that stands for “ϕ holds after all informative events” — the diamond version ∃ϕ stands for “there is an informative event after which ϕ.” The proposal ...
Introduction to mathematical reasoning Chris Woodward Rutgers
... 17.3. Real numbers as equivalence classes of Cauchy sequences 17.4. Existence of suprema and infima 17.5. Base representations of real numbers 17.6. Cantor’s uncountability argument References ...
... 17.3. Real numbers as equivalence classes of Cauchy sequences 17.4. Existence of suprema and infima 17.5. Base representations of real numbers 17.6. Cantor’s uncountability argument References ...
Theory of L-functions - Institut für Mathematik
... number theory) correspond one-to-one to product identities of Dirichlet series. This leads via (formal) differentiation to new identities for arithmetic functions from old ones. Furthermore, in many cases one can exhibit number theoretical information from identities for the associated Dirichlet ser ...
... number theory) correspond one-to-one to product identities of Dirichlet series. This leads via (formal) differentiation to new identities for arithmetic functions from old ones. Furthermore, in many cases one can exhibit number theoretical information from identities for the associated Dirichlet ser ...
Lecture 15 - Mathematics
... Let S be a set of k-tuples (s1 , s2 , . . . , sk ) of objects in which: the rst object s1 comes from a set of size n1 for each choice of s1 there are n2 choices for object s2 for each choice of s2 there are n3 choices for object s3 for each choice of s3 there are n4 choices for object s4 and, in ge ...
... Let S be a set of k-tuples (s1 , s2 , . . . , sk ) of objects in which: the rst object s1 comes from a set of size n1 for each choice of s1 there are n2 choices for object s2 for each choice of s2 there are n3 choices for object s3 for each choice of s3 there are n4 choices for object s4 and, in ge ...
Symbmath - Computer Algebra System for Symbolic Computation
... and graphic computation. It manipulates complicated formulas and returns answers in terms of symbols, formulas, exact numbers, tables and graph. SymbMath is an expert system that is able to learn from user's input. If the user only input one formula without writing any code, it will automatically le ...
... and graphic computation. It manipulates complicated formulas and returns answers in terms of symbols, formulas, exact numbers, tables and graph. SymbMath is an expert system that is able to learn from user's input. If the user only input one formula without writing any code, it will automatically le ...