quadratic - James Tanton
... If we denote the length of one side of the quadrangle as x units, then the other must be x + 4 units in length. We must solve the equation: x ( x + 4) = 60 , which is equivalent to solving the quadratic equation x 2 + 4 x − 60 = 0 . Solving quadratic equations, even if not derived from a quadrangle ...
... If we denote the length of one side of the quadrangle as x units, then the other must be x + 4 units in length. We must solve the equation: x ( x + 4) = 60 , which is equivalent to solving the quadratic equation x 2 + 4 x − 60 = 0 . Solving quadratic equations, even if not derived from a quadrangle ...
Use your book (starting on page 218) to complete the notes for
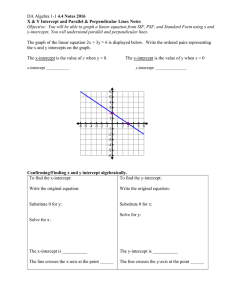
... 1) For lines to be parallel, what must be true about their slopes?_________________________ 2) Give an example of two slopes that are parallel. _________________ 3) For lines to be perpendicular, what must be true about their slopes?__________________________ 4) Give an example of two slopes that ar ...
... 1) For lines to be parallel, what must be true about their slopes?_________________________ 2) Give an example of two slopes that are parallel. _________________ 3) For lines to be perpendicular, what must be true about their slopes?__________________________ 4) Give an example of two slopes that ar ...
notes
... Triangle Medians A median of a triangle is a line segment drawn from any vertex of the triangle to the midpoint of the opposite side. B Question: If I printed this slide in black and white, what would be incorrect about the figure? ...
... Triangle Medians A median of a triangle is a line segment drawn from any vertex of the triangle to the midpoint of the opposite side. B Question: If I printed this slide in black and white, what would be incorrect about the figure? ...
Orbits of rotor-router operation and stationary distribution of
... ρ means the process of updating ρ(v) to ρ(v)+ , and then the chip moves along the updated edge ρ(v) to the head. The chip is now at the head of the edge ρ(v). We define a single-chip-and-rotor state (often briefly state) to be a pair (v, ρ) of a vertex and a rotor configuration ρ of G. The vertex v ...
... ρ means the process of updating ρ(v) to ρ(v)+ , and then the chip moves along the updated edge ρ(v) to the head. The chip is now at the head of the edge ρ(v). We define a single-chip-and-rotor state (often briefly state) to be a pair (v, ρ) of a vertex and a rotor configuration ρ of G. The vertex v ...
DISTANCE EDUCATION M.Phil. (Mathematics) DEGREE
... Answer any FIVE questions. All questions carry equal marks. ...
... Answer any FIVE questions. All questions carry equal marks. ...
Chapter 1 Section 4: Compound Linear Inequalities Introduction
... You’ve already encountered one type of compound inequality in the "Sets, Interval Notation, and Linear Inequalities" section—the three-way inequality. This section goes beyond that type of compound inequality. When we write A < x < B , we mean that A < x and also that x < B . In other words, x is in ...
... You’ve already encountered one type of compound inequality in the "Sets, Interval Notation, and Linear Inequalities" section—the three-way inequality. This section goes beyond that type of compound inequality. When we write A < x < B , we mean that A < x and also that x < B . In other words, x is in ...
UNIT &
... choosing any value of x and f inding the corresponding value of y. Repeat this procedure, choosing different values for x, unttl you have found the number of solutions desired. ...
... choosing any value of x and f inding the corresponding value of y. Repeat this procedure, choosing different values for x, unttl you have found the number of solutions desired. ...
Using Ontology Graphs to Understand Annotations and Reason about Them
... standards to meet the needs of their community, one of the important results of various ontology projects has been an attempt to develop a common vocabulary and shared annotation standards that enhance the utility of these annotations for analysis. We have found that regardless of the ontology, pres ...
... standards to meet the needs of their community, one of the important results of various ontology projects has been an attempt to develop a common vocabulary and shared annotation standards that enhance the utility of these annotations for analysis. We have found that regardless of the ontology, pres ...
solution of a linear inequality
... Additional Example 3b Continued b. Graph the solutions. Step 2 Shade below the line. Ada can only make whole numbers of jewelry. All points on or below the line with whole number coordinates are the different combinations of bracelets and necklaces that Ada can make. ...
... Additional Example 3b Continued b. Graph the solutions. Step 2 Shade below the line. Ada can only make whole numbers of jewelry. All points on or below the line with whole number coordinates are the different combinations of bracelets and necklaces that Ada can make. ...
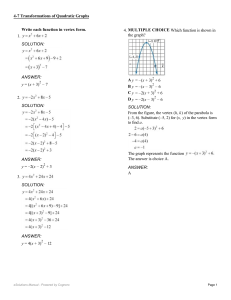
Write each function in vertex form. 1. SOLUTION: ANSWER: y = (x +
... SOLUTION: Sample answer: The variable a represents different values for these functions, so making a = 0 will have a different effect on each function. For f (x), when a = 0, the graph will be a horizontal line, f (x) = k. For g (x), when a = 0, the graph will be linear, but not necessarily horizo ...
... SOLUTION: Sample answer: The variable a represents different values for these functions, so making a = 0 will have a different effect on each function. For f (x), when a = 0, the graph will be a horizontal line, f (x) = k. For g (x), when a = 0, the graph will be linear, but not necessarily horizo ...
A Short Proof that “Proper = Unit”
... assignment is an interval representation. When the intervals have the same length, we have a unit interval representation. When no interval properly contains another, we have a proper interval representation. The unit interval graphs and proper interval graphs are the interval graphs having unit int ...
... assignment is an interval representation. When the intervals have the same length, we have a unit interval representation. When no interval properly contains another, we have a proper interval representation. The unit interval graphs and proper interval graphs are the interval graphs having unit int ...
U.S. NAVAL ACADEMY COMPUTER SCIENCE DEPARTMENT TECHNICAL REPORT Algorithmic Reformulation of Polynomial Problems
... Rewritings with constants, known redundancies, or inconsistencies are not “interesting”. Point 1 of the definition means we don’t allow constants, points 1 & 4 mean that we don’t allow distinct but obviously equivalent Q-nodes, and point 3 means we don’t allow distinct but obviously equivalent OR-n ...
... Rewritings with constants, known redundancies, or inconsistencies are not “interesting”. Point 1 of the definition means we don’t allow constants, points 1 & 4 mean that we don’t allow distinct but obviously equivalent Q-nodes, and point 3 means we don’t allow distinct but obviously equivalent OR-n ...
2.1 The Distance and Midpoint Formulas The distance d(A,B
... A solution of an equation in two variables is a pair of numbers that satisfies the equation, that is, it makes the equation true. The graph of an equation in two variables is the set of all points (x,y) in the coordinate system such that the pair (x,y) is a solution of the equation. Example : Check ...
... A solution of an equation in two variables is a pair of numbers that satisfies the equation, that is, it makes the equation true. The graph of an equation in two variables is the set of all points (x,y) in the coordinate system such that the pair (x,y) is a solution of the equation. Example : Check ...
Graph Summarization in Annotated Data Using
... observe that the two gene nodes share four out of their five neighbors, which can still be viewed as a relatively strong indication to cluster them. Next, we consider explicit similarities between pairs of nodes. Such additional information could help deciding whether the third GO term should be in ...
... observe that the two gene nodes share four out of their five neighbors, which can still be viewed as a relatively strong indication to cluster them. Next, we consider explicit similarities between pairs of nodes. Such additional information could help deciding whether the third GO term should be in ...
Median graph
In graph theory, a division of mathematics, a median graph is an undirected graph in which every three vertices a, b, and c have a unique median: a vertex m(a,b,c) that belongs to shortest paths between each pair of a, b, and c.The concept of median graphs has long been studied, for instance by Birkhoff & Kiss (1947) or (more explicitly) by Avann (1961), but the first paper to call them ""median graphs"" appears to be Nebeský (1971). As Chung, Graham, and Saks write, ""median graphs arise naturally in the study of ordered sets and discrete distributive lattices, and have an extensive literature"". In phylogenetics, the Buneman graph representing all maximum parsimony evolutionary trees is a median graph. Median graphs also arise in social choice theory: if a set of alternatives has the structure of a median graph, it is possible to derive in an unambiguous way a majority preference among them.Additional surveys of median graphs are given by Klavžar & Mulder (1999), Bandelt & Chepoi (2008), and Knuth (2008).