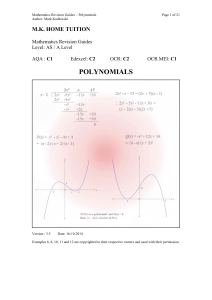
polynomials - MK Home Tuition
... This time, there is a final remainder, namely -19. So x3 - 7x2 + 6x - 1 = (x –3)(x2 - 4x - 6) - 19. The Remainder Theorem. In Example (4) above we divided x3 - 7x2 + 6x - 1 by x –3 to give a quotient of x2 - 4x - 6 and a remainder of -19. Another way to find out the remainder is to substitute certai ...
... This time, there is a final remainder, namely -19. So x3 - 7x2 + 6x - 1 = (x –3)(x2 - 4x - 6) - 19. The Remainder Theorem. In Example (4) above we divided x3 - 7x2 + 6x - 1 by x –3 to give a quotient of x2 - 4x - 6 and a remainder of -19. Another way to find out the remainder is to substitute certai ...
cis667-10
... • The reversal distance of oriented permutations is given by: • d(a) = n + 1 - c(a) + h(a) + f(a) c(a) - number of cycles (proper and non) h(a) - number of hurdles f(a) - a a fortress? (1 else 0) n + 1 - c(a) good components and bad components ...
... • The reversal distance of oriented permutations is given by: • d(a) = n + 1 - c(a) + h(a) + f(a) c(a) - number of cycles (proper and non) h(a) - number of hurdles f(a) - a a fortress? (1 else 0) n + 1 - c(a) good components and bad components ...
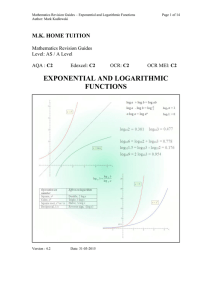
Exponential and Logarithmic Functions
... EXPONENTIAL AND LOGARITHMIC FUNCTIONS An exponential function is one whose variable is a power or exponent. Any function of the form f (x) = ax , where a is a non-zero positive constant, is an exponential function. The graphs on the right are of two such exponential functions: y = 2x and y = 5x. All ...
... EXPONENTIAL AND LOGARITHMIC FUNCTIONS An exponential function is one whose variable is a power or exponent. Any function of the form f (x) = ax , where a is a non-zero positive constant, is an exponential function. The graphs on the right are of two such exponential functions: y = 2x and y = 5x. All ...
Lesson 4-2
... Trish can run the 200 m dash in 25 s. The function f(x) = 200 – 8x gives the distance remaining to be run after x seconds. Graph this function and find the intercepts. What does each intercept represent? ...
... Trish can run the 200 m dash in 25 s. The function f(x) = 200 – 8x gives the distance remaining to be run after x seconds. Graph this function and find the intercepts. What does each intercept represent? ...
4-2
... Trish can run the 200 m dash in 25 s. The function f(x) = 200 – 8x gives the distance remaining to be run after x seconds. Graph this function and find the intercepts. What does each intercept represent? ...
... Trish can run the 200 m dash in 25 s. The function f(x) = 200 – 8x gives the distance remaining to be run after x seconds. Graph this function and find the intercepts. What does each intercept represent? ...
(slides)
... C ∗ (E , L) ×αe,r G ∼ = C ∗ (E /G , L/G ) ⊗ K(`2 (G )) we need two theorems. The Gross-Tucker theorem for labeled graphs: a free action on a labeled graph is naturally equivariantly isomorphic to a skew product action obtained from the quotient labeled graph. A generalization of a theorem of Kalisze ...
... C ∗ (E , L) ×αe,r G ∼ = C ∗ (E /G , L/G ) ⊗ K(`2 (G )) we need two theorems. The Gross-Tucker theorem for labeled graphs: a free action on a labeled graph is naturally equivariantly isomorphic to a skew product action obtained from the quotient labeled graph. A generalization of a theorem of Kalisze ...
cloudfront.net
... Make a Prediction Suppose you started by constructing the set of points equidistant from P and Q and then constructed the set of points equidistant from Q and R. Would you have found the same center? Check by doing this construction. ...
... Make a Prediction Suppose you started by constructing the set of points equidistant from P and Q and then constructed the set of points equidistant from Q and R. Would you have found the same center? Check by doing this construction. ...
Log Functions I
... Justification: The domain of the log function is the range of an exponential function since these two functions are inverses. Notice that we do not include 0 in the domain because exponential functions do not return the value 0. The range of the log function is the domain of the exponential function ...
... Justification: The domain of the log function is the range of an exponential function since these two functions are inverses. Notice that we do not include 0 in the domain because exponential functions do not return the value 0. The range of the log function is the domain of the exponential function ...
Generalized honeycomb torus
... where n is even. The honeycomb rhombic torus HRoT(m, n) is the graph with the node set {(i, j ) | 0 i
... where n is even. The honeycomb rhombic torus HRoT(m, n) is the graph with the node set {(i, j ) | 0 i
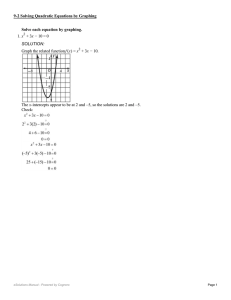
Solve each equation by graphing. 1. x + 3x − 10 = 0 SOLUTION
... This graph has no x-intercepts. Therefore, this equation has no real number solutions. The solution set is {∅}. Check: There are no factors of 9 that have a sum of 0, so the expression is not factorable. Thus, the equation has no real number solutions. ...
... This graph has no x-intercepts. Therefore, this equation has no real number solutions. The solution set is {∅}. Check: There are no factors of 9 that have a sum of 0, so the expression is not factorable. Thus, the equation has no real number solutions. ...
standard form equation of a hyperbola
... a. If the transverse axis is oriented horizontally, the conjugate axes are (h,k+b) and (h,k–b). b. If the transverse axis is oriented vertically, the conjugate axes is (h+b,k) and (h–b,k). 5. Construct a box that passes through the both vertices and the points marking the conjugate ...
... a. If the transverse axis is oriented horizontally, the conjugate axes are (h,k+b) and (h,k–b). b. If the transverse axis is oriented vertically, the conjugate axes is (h+b,k) and (h–b,k). 5. Construct a box that passes through the both vertices and the points marking the conjugate ...
Median graph
In graph theory, a division of mathematics, a median graph is an undirected graph in which every three vertices a, b, and c have a unique median: a vertex m(a,b,c) that belongs to shortest paths between each pair of a, b, and c.The concept of median graphs has long been studied, for instance by Birkhoff & Kiss (1947) or (more explicitly) by Avann (1961), but the first paper to call them ""median graphs"" appears to be Nebeský (1971). As Chung, Graham, and Saks write, ""median graphs arise naturally in the study of ordered sets and discrete distributive lattices, and have an extensive literature"". In phylogenetics, the Buneman graph representing all maximum parsimony evolutionary trees is a median graph. Median graphs also arise in social choice theory: if a set of alternatives has the structure of a median graph, it is possible to derive in an unambiguous way a majority preference among them.Additional surveys of median graphs are given by Klavžar & Mulder (1999), Bandelt & Chepoi (2008), and Knuth (2008).