Download stats_6_3_1

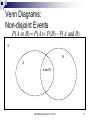
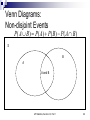
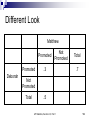
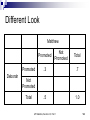
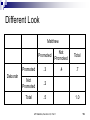
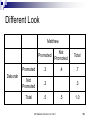
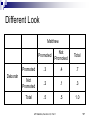
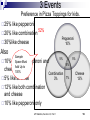
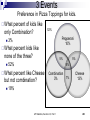
Warm Up

Chapter 6.2 Quiz Today
1.
What is the probability of choosing an Ace,
with out returning it, and then a King from a
deck of cards? Assume the deck has 52 cards.
2.
Redo #1 but this time return the card.
AP Statistics, Section 6.3, Part 1
2
Section 6.3.1
Probability Models
AP Statistics
Venn Diagrams: Disjoint Events
S
A
B
S = (sample space=all possible outcomes.)
Not the same as
Independent:
Independent events
must be able to occur
at the same time. If
one happens, it has
no influence on the
other whatsoever.
The occurrence of
one provides no
information about the
other.
4
Independent vs Disjoint

The occurrence of one provides no information about the other.
Ex: You place a bet on a card being red.
 I peak and tell you it’s an ace. Does that help
you? Before you knew this, the probability the
card is red was 26/52 = 1/2. Knowing it’s an
ace, the probability it’s red is 2/4 = 1/2. No help
whatsoever – the probability has not changed.
These two events ARE independent (and not
disjoint). P(red | ace) = P(red) — that’s the very
definition of independence:
the occurrence of “ace” has no effect on the
probability of “red”.

5
Venn Diagrams: Disjoint Events
P( A or B)  P( A)  P( B)
S
A
B
AP Statistics, Section 6.3, Part 1
6
Venn Diagrams:
Non-disjoint Events
P( A or B)  P( A)  P( B)  P( A and B)
S
B
A
A and B
AP Statistics, Section 6.3, Part 1
7
Venn Diagrams:
Non-disjoint Events
P( A  B)  P( A)  P( B)  P( A  B)
S
B
A
A and B
AP Statistics, Section 6.3, Part 1
8
Example

Deborah and Matthew are awaiting the
decision about a promotion. Deborah
guesses her probability of her getting a
promotion at .7 and Matthew’s probability
at .5.
AP Statistics, Section 6.3, Part 1
9
Example

Deborah and Matthew
are awaiting the
decision about a
promotion. Deborah
guesses her
probability of her
getting a promotion at
.7 and Matthew’s
probability at .5.
D
.7
AP Statistics, Section 6.3, Part 1
M
.5
10
Example

Since there is not
enough information to
do the problem, let’s
add information.
Deborah thinks the
probability of both
getting promoted is .3
.1
D
.4
.7
AP Statistics, Section 6.3, Part 1
D and M
.3
M
.5
.2
11
Example
.1





What’s the probability
of only Deborah
getting promoted
P(D-M)?
P(M-D)?
P(Dc)?
P(Mc)?
P(Dc and Mc)?
D
.4
AP Statistics, Section 6.3, Part 1
D and M
.3
M
.2
12
Different Look
Matthew
Promoted
Promoted
Deborah
Not
Promoted
.3
Total
.7
Not
Promoted
Total
.5
AP Statistics, Section 6.3, Part 1
13
Different Look
Matthew
Promoted
Promoted
Deborah
Not
Promoted
Total
.3
.7
.5
1.0
Not
Promoted
Total
AP Statistics, Section 6.3, Part 1
14
Different Look
Matthew
Deborah
Promoted
Not
Promoted
Total
Promoted
.3
.4
.7
Not
Promoted
.2
Total
.5
AP Statistics, Section 6.3, Part 1
1.0
15
Different Look
Matthew
Deborah
Promoted
Not
Promoted
Total
Promoted
.3
.4
.7
Not
Promoted
.2
Total
.5
AP Statistics, Section 6.3, Part 1
.3
.5
1.0
16
Different Look
Matthew
Deborah
Promoted
Not
Promoted
Total
Promoted
.3
.4
.7
Not
Promoted
.2
.1
.3
Total
.5
.5
1.0
AP Statistics, Section 6.3, Part 1
17
3 Events
Preference in Pizza Toppings for
 25%
like pepperoni
 20% like combination
 30% like cheese
Whole circle
needs to
kids.
add up to
25%
Pepperoni
Also
 10%
like both pepperoni and
cheese
Combination
 5% like all three
 12% like both combination
and cheese
 10% like pepperoni only Whole circle
needs to add
up to 20%
AP Statistics, Section 6.3, Part 1
Cheese
Whole circle
needs to add
up to 30%
18
3 Events
Preference in Pizza Toppings for kids.
 25%
like pepperoni
52%
 20% like combination
 30%like cheese
Pepperoni
10%
Also
Sample
Space
Mustpepperoni
 10% like
both
Add Up to
cheese100%
 5%
and
like all three
 12% like both combination
and cheese
 10% like pepperoni only
Combination
3%
AP Statistics, Section 6.3, Part 1
5%
5%
5%
7%
Cheese
13%
19
3 Events
Preference in Pizza Toppings for kids.
 What
percent of kids like
only Combination?

52%
Pepperoni
10%
3%
 What
percent kids like
none of the three?

52%
 What
5%
percent like Cheese
but not combination?

5%
5%
Combination
3%
7%
Cheese
13%
18%
AP Statistics, Section 6.3, Part 1
20
Using a Venn Diagram
 The
probability of event A
happening is .64
.28
 The Probability of event B
happening is .20
 The probability of both
events occurring is .12.
 What
is the probability of
each event.
A and B =.12
 A and Bᶜ =.52
=.08
 Aᶜ and B
 Aᶜ and Bᶜ =.28
A
.52
B
.12
.08

AP Statistics, Section 6.3, Part 1
21
Assignment

Exercises: 6.46-6.53, all
AP Statistics, Section 6.3, Part 1
22