Download Chapter 2.3 the use of statistics in psychology

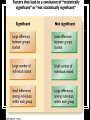
the use of
statistics in
psychology
statistics
 Essential
 Occasionally
misleading
Two types
– mathematical
summaries of results
 Descriptive
– statements about large
populations derived from small
samples
 Inferential
Descriptive
statistics

Measures of the central score

Mean – the average score, found by
adding all the scores together and then
dividing by the number of scores
Vulnerable to skewing by very high scores
Measures of the
central score ii

Median – the middle score after the
scores are arranged from highest to lowest

Much less sensitive to skewing
Central score
measures iii


Mode – the most common score
Usually of limited interest
Measures of
variation



Enough about the “central score”, how the
scores differ, or vary, within a distribution is
just as important
The Range – the difference between the
highest and lowest score
The Standard Deviation – a measurement
of the amount of variation among scores in
a normal distribution
examples

Sample distribution – 1,2,3,3,21

Measures of Central Score
Mean = 6
Median = 3

Variation
Range = 20
Standard Deviation = 7.5
Mode = 3
Inferential
statistics



We found a difference between the
experimental group and the control group.
What does that tell us about the population
we are interested in?
Could the difference have resulted from
chance?
Inferential
statistics ii


Procedures used to decide whether
differences really exist between sets of
numbers
Does our experimental group significantly
differ from the population from which it was
drawn?
significance tests



Assess the odds that we could have gotten
such a difference (between the
experimental and the control group) at
random
We want to prove that the difference would
only occur 5% of the time by luck
If we can, then the difference is significant
– our experiment worked.
Data set 1








Experimental group
3
10
10
10
2
35
Mean=7; SD=4.1








Control group
5
7
6
5
7
30
Mean= 6; SD= 1
Inferential
statistics

Statements about large populations taken
from small samples

How can we be sure that our results really
mean something?
That they apply to the entire population and
not just to the sample?

data set 2












Experimental group
10
6
7
9
8
7
10
8
Mean = 8
6
SD = 1.5
9
80












Control group
7
6
5
10
2
4
8
6
Mean = 6
5
SD = 2.2
7
60
In other words…


If the experimental group’s free throw
shooting performance had not been
affected by the relaxation technique, we
would only see such a difference between
the two groups in 1 out of 500 occasions.
We can reasonably claim that the results
supported our hypothesis.