Download Data Analysis

Data
Freshman Clinic II
Overview










Populations and Samples
Presentation
Tables and Figures
Central Tendency
Variability
Confidence Intervals
Error Bars
Student t test
Linear Regression
Applications
Populations and Samples

Population
– All possible data points



Entire US population
Every rainfall event in Glassboro (past, present, and
future)
Sample
– Subset of population

We use samples to estimate population
parameters
Presentation
Present clearly, objectively
 Properly communicate uncertainty
 Compare using valid statistics

Tables
Table 1: Water Quality (average of 3 to 5 values)
a
b
Water
Turbidity
(NTU)
True Color
(Pt-Co)
(1)
Pond Water
(2)
10
(3)
13
Apparent
Color
(Pt-Co)
(4)
30
Sweetwater
4
5
12
Hiker
3
8
11
MiniWorks
2
3
5
Comparison
5a
15b
15b
Visually detectable
Drinking Water Standard
Figures – Bar Chart
25
Turbidity (NTU)
20
20
11
15
10
11
10
7
5
5
1
0
Pond Water Sweetwater
Miniworks
Hiker
Pioneer
Voyager
Filter
Figure 1: Average Turbidity of Pond Water, Treated and Untreated
Apparent Color (Pt-Co)
Figures – XY Scatter
18
16
14
12
10
8
6
4
2
0
0
2
4
6
8
Water Treated (L)
Figure 2: Change in Water Quality
10
Central Tendency

Example: Turbidity of Treated Water (NTU)
– Sample is 1, 3, 3, 6, 8, 10
n=6
Mean = Sum of values divided by number of data points
e.g., (1+3+3+6+8+10)/6 = 5.17 NTU
Median = The middle number
Rank 1 2 3 4 5 6
Number 1 3 3 6 8 10 (ordered)
For even number of sample points, average middle two
e.g., (3+6)/2 = 4.5
For odd number of sample points, median = middle point
Variability

Standard deviation of a sample
 x  x 
2
s
i
n 1
xi = ith data point
x = mean of sample
n = number of data points
e.g.,
[{(1-5.2)2+(3-5.2)2 +(3-5.2)2 +(6-5.2)2 +(8-5.2)2 +(10-5.2) 2}/(6-1)]0.5
= 3.43
Confidence Interval of Mean

Estimated range within which population mean falls
– e.g., 95% confidence interval of mean, based on our
sample, is (1.57    8.77) where  = population mean
– We are 95% confident true mean of population (from
which our sample was drawn) lies within this range

Confidence interval (CI) calculated from sample:
ts
CI  x 
n
Where x = sample mean, t = statistical parameter related to
confidence, s = sample standard deviation, and n = sample size
Calculating “t”



In Excel, type “=TINV” into
a cell and select the “=“
symbol in the formula bar
The student’s t-distribution
inverse formula palette
pops up
“Probability” = 1 –
confidence level (as a
fraction)
– e.g., if confidence level is
95%, “probability” = 1 - 0.95
= 0.05

“Deg_freedom” = degrees
of freedom = n - 1

TINV returns “t”, the
statistical parameter
we need to estimate a
confidence interval
based on a sample
Calculating a Confidence Interval

For our example:
– “TINV” returned 2.57
– t x s / sqrt(n) = 2.57 x 3.43 / sqrt(6) = 3.60


5.17 – 3.60 = 1.57
5.17 + 3.60 = 8.77
– CI: (1.57    8.77) with 95% confidence


i.e., we are 95% confident the population mean lies
between 1.57 and 8.77
Quite Wide!
– Lower “s” or higher “n” will narrow range
Error Bars

Used to show data variability on a graph
30
Turbidity (NTU)
25
20
15
10
5
0
Pond Water
Sweetwater
Water (Untreated and Treated)

Bar chart, XY,…
Miniworks
Types of Error Bars
Standard Error of Mean
 Confidence Interval
 Standard Deviation
 Percentage

http://www.graphpad.com/articles/errorbars.htm
Standard Error
s
n
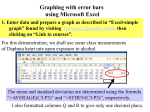
Adding Error Bars
1.
2.
3.
Create chart in Excel
Select a data series by
selecting a data point or bar
From “Format” menu, select
“Selected data series…”
5. Select + and – error bar
data. This could be standard
deviation, standard error, or
confidence limits.
4. Select “custom”
Confidence Interval
Average Lower
Upper
Turbidity Interval Interval
Pond Water
20
4
4
Sweetwater
10
2
2
Miniworks
7
3
3
Error Bars and our Example
Standard Error of Mean
 s / sqrt(n) = 3.43 / sqrt(6) = 1.40
 Put 1.40 in + and - cells
 Since the mean = 5.17, the error bars in a
bar chart would go from

– 5.17 – 1.40 = 3.77 to
– 5.17 + 1.40 = 6.57
Interpreting Error Bars


Error bars can be used to compare
two sample means
Standard Error (SE)
– SE bars do not overlap, no conclusions
can be drawn
– SE bars overlap, sample appear to be
not drawn from significantly different
populations

Confidence Interval (CI)
– CI bars do not overlap, samples appear
to be drawn from significantly different
populations, at confidence level of
confidence interval
– CI bars overlap, no conclusions can be
drawn
http://www.graphpad.com/articles/errorbars.htm
Comparing Samples with a t-test

Example - You measure untreated and
treated pond water
– Treated: mean = 2 NTU, s = 0.5 NTU, n = 20
– Untreated: mean = 3 NTU, s = 0.6 NTU, n = 20

You ask the question – Is the average
turbidity of treated water different from that
of untreated water?
– Use a t-test
Is the water different?

Use TTEST (Excel)
Probability (as fraction) of being wrong if you claim
statistically significant difference (type I error)

–Select significance level ahead of time, usually 0.01 - 0.1
–For our example, our #, 0.0000015, is very small
Treated
1.5
2
2.2
1.8
3
1.6
1.2
2.1
1.9
2.2
2.6
1.7
1.8
1.5
2.4
2.5
2.7
1.4
1.5
2.6
Untreated
3
2.4
2.2
2.6
3.4
3.6
3.8
3.5
2.7
2.4
3.5
3.8
2.1
2.5
3.4
3.3
2.4
3.6
2.3
3.7
T test steps
1. Identify two samples to compare
2. Select a , significance of statistical test
–
–
We’ll use 0.05 in this class
Confidence = 1 - a
3. Use Excel “TTEST” formula to estimate probability
of Type I Error
4. If probability returned by TTEST is less than or
equal to 0.05, assume the samples come from
two different populations
For our example, 0.0000015 < 0.05, assume the treated
water is different from the untreated water
Linear Regression

Fit the best straight line to a data set
Grade Point Average
25
20
y = 1.897x + 0.8667
R2 = 0.9762
15
10
5
0
0
2
4
6
8
10
12
Height (m)
Right-click on data point and use “trendline” option. Use “options”
tab to show equation and R2.
R2 - Coefficient of multiple Determination
R
ŷi
y
yi
R2
2
 yˆ


y
 y
2
i
 y
2
i
= Predicted y values, from regression equation
= Average of y
= Observed y values
= fraction of variance explained by regression
(variance = standard deviation squared)
= 1 if data lies along a straight line
What might you do in this class?

Flow rate versus stroke rate
– Figure with linear regression over linear range

Ability to improve water quality
– Table and t-test comparison with untreated water (for turbidity and
apparent color), or
– Bar chart (for turbidity and apparent color) with confidence interval
error bars

Pressure change versus flow rate, Power versus flowrate
– Figure (no statistics possible because we only took one reading of
pressure for each flow rate and relationship is non-linear)

Force versus stroke rate,
– Figure w/95% confidence interval error bars for each data point

Power versus Flowrate
– Figure
Example – Water Quality
Table 2: Improvement in Water Quality
Untreated Water
Treated Water
Statistically
Mean Standard Mean Standard Significant
Deviation
Deviation Difference?
Turbidity, NTU
8
1
3
0.5
Yes
Apparent Color, Pt-Co
100
5
7
0.6
Yes
Note: Statistical significance tested at level = 0.05 using t-test