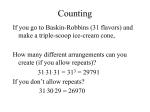Download Probability and Statistics - Math GR. 6-8

Probability and Statistics
Teacher Quality Grant
What do you know about probability?
• Probability is a number from 0 to 1 that tells
you how likely something is to happen.
• Probability can have two approaches
Experimental probability
- Theoretical probability
-
Key Words
• Experimental probability
• Theoretical probability
• Law of Large Numbers
• Outcome
• Event
• Random
Click here to check the words
Definition of Probability
• Probability is a measure of how likely it is
for an event to happen.
• The probability of one or more events is a
number between 1 and 0
• The notation for and event is P(event)
Probability
P=0
Event will
never occur
1
2
Event is equally
likely to occur or
not occur

P=
P=1
Event will
always occur
Chance / Probability
• When a meteorologist states that the
chance of rain is 50%, the meteorologist is
saying that it is equally likely to rain or not
to rain. If the chance of rain rises to 80%, it
is more likely to rain. If the chance drops to
20%, then it may rain, but it probably will
not rain.
Probability Activity 1
• The probability of an event happening can
be expressed as a percent between 0% and
100%. The probability of an event that is
impossible is expressed as 0%. The
probability of an event that is certain to
happen is expressed as 100%.
Probability Activity 1
• The table below shows a seven-day weather forecast,
including the probability of precipitation (POP). The event
in this case is rain, and the probability is a number
expressed as a percent between 0% and 100%.
Probability Activity 1
1. For which days does the forecast indicate no possibility of rain?
• Sunday, Monday, and Saturday
2. For which day does the forecast indicate that rain is as likely to
happen as not?
• Wednesday
3. On which day is it more likely to rain, Thursday or Friday?
• Friday
4. On which day is it less likely to rain, Tuesday or Thursday?
• Tuesday
Probability Activity 1
5. Discuss whether the amount of rain on Tuesday (POP 15%) could
be greater than the amount of rain on Thursday (POP 20%),
assuming that it rains on both days.
Experimental vs. Theoretical
Experimental probability:
P(event) = number of times event occurs
total number of trials
Theoretical probability:
P(E) = number of favorable outcomes
total number of possible outcomes
THEORETICAL PROBABILITY
THE THEORETICAL PROBABILITY OF AN EVENT
The theoretical
probability
of anlikely,
eventthe
is
When
all outcomes
are equally
often simplyprobability
called the probability
of theA event.
theoretical
that an event
will occur is:
P (A) =
number of outcomes in A
total number of outcomes
all possible
outcomes
P (A) = 4
9
outcomes
in event A
You can express a probability as a fraction, a decimal, or
a percent.
For example: 1 , 0.5, or 50%.
2
Theoretical probability
HEADS
TAILS
P(head) = 1/2
P(tail) = 1/2
Since there are only
two outcomes, you
have 50/50 chance
to get a head or a
tail.
Theoretical probability
B A
C D
3
1
2
1. What is the probability that the spinner will
stop on part A?
2. What is the probability that the spinner
will stop on
(a) An even number?
(b) An odd number?
A
C
B
3. What fraction names the
probability that the spinner will stop in
the area marked A?
Probability Activity 2
• In your group, open your M&M bag and put the candy on
the paper plate.
• Put ten brown M&Ms and five yellow M&Ms in the bag.
• Ask your group, what is the probability of getting a brown
M&M?
• Ask your group, what is the probability of getting a yellow
M&M?
• Another person in the group will then put in 8 green M&Ms
and 2 blue M&Ms.
• Ask the group to predict which color you are more likely to
pull out, least likely, unlikely, or equally likely to pull out.
• The last person in the group will make up his/her own
problem with the M&Ms.
Finding Probabilities of Events
You roll a six-sided number cube whose sides are numbered
from 1 through 6.
Find the probability of rolling a 4.
SOLUTION
Only one outcome corresponds to rolling a 4.
1
number of ways to roll a 4
P (rolling a 4) =
= 6
number of ways to roll the die
Finding Probabilities of Events
You roll a six-sided number cube whose sides are numbered
from 1 through 6.
Find the probability of rolling an odd number.
SOLUTION
Three outcomes correspond to rolling an odd number:
rolling a 1, 3, or a 5.
P (rolling odd number) =
3
number of ways to roll an odd number
=
6
number of ways to roll the die
=
1
2
Probability of multiple Events
• First you must determine if the events are
independent or dependent
• Independent events: Events that do not affect one
another.
• Dependent events: When the first event affects the
probability of the other(s).
Event 1
• Events that do not have an effect on one
another.
If we are choosing 2 cards from a
deck and after we choose the first
card we replaces it shuffle and
choose again.
Does the first pick affect the second?
No, so this means the 2 events are independent.
Event 2
• Events that do not have an effect on one
another.
If we are choosing 2 cards from a
deck and after we choose the first
card we do not replaces it, we just
choose again.
Does the first pick affect the second?
Yes because there are less card now,
so this means the 2 events are dependent.
A Deck of cards
Are the events Independent or
Dependent Events?
• Rolling 3 number cubes
– Independent: one number does not affect the others
• Choosing 2 marbles from a bag with out
replacement.
– Dependent: each time you choose you have one less
marble
Are the events Independent or
Dependent Events?
• Rolling a number cube and flipping a coin
– Independent: the number cube does not affect the coin
Counting outcomes of multiple
events
• Making a list
• Tree Diagrams
• Quick multiplication
• Combination and Permutation
Making a list
A B C D
E
F
G
• PROBLEM: Phillip will shuffle the cards
and choose three without looking or
replacing them. How many different
combinations are possible?
Making a list
A B C D
E
F
G
• When making a list start with the first
letter and list all possibilities using that
letter.
ABC
ABD
ABE
ABF
ABG
ACB
ACD
ACE
ACF
ACG
ADB
ADC
ADE
ADF
ADG
AEB
AEC
AED
AEF
AEG
Does order matter? No
Can we eliminate any? Yes
AFB
AFC
AFD
AFE
AFG
AGB
AGC
AGD
AGE
AGF
Making a list
A B C D
E
F
G
• When making a list start with the first
letter and list all possibilities using that
letter.
ABC
ABD
ABE
ABF
ABG
ACD
ACE
ACF
ACG
ADE
ADF
ADG
AEF
AEG
AFG
How many combinations are left?
15
Making a Tree Diagram
• A tree diagram is an
image made up of a
branching structure,
which is used to
show connections
between items,
topics or ideas.
Making a Tree Diagram
• In Probability or Data analysis we use a
tree diagram to show all possible
outcomes for a given situation.
Making a Tree Diagram
• To make a tree diagram we must begin
by identifying the first stage or choice.
Making a Tree Diagram
Example:
You sit down at a restaurant for a meal and
on the menu there are 3 salads 4 main
courses and 3 deserts. How many
different 3 course meals are possible.
Salads
Main courses
Deserts
Salads
Main courses
Deserts
A
1
2
3
B
1
1
2
3
1
2
3
C
1
2
3
D
A
1
2
3
B
2
C
D
A
3
1
2
3
B
C
D
1
2
3
1
2
3
1
2
3
1
2
3
1
2
3
1
2
3
Activity 3: Tree Diagram
• Get into groups of 3
• In each group you are to design a tree
diagram on your poster paper.
• Make sure to include a key if you are
using acronyms.
• Activity is also included
Activity 4: Permutations
Sample Situation
Ms. Jones uses the four letters A, B, C, and
D in different orders to assign computer
log-in passwords to her 20 students. Each
letter appears only once in a password, but
the order of the letters can be different.
Activity 4: Permutations
1. Complete the tables by forming four-letter passwords.
Activity 4: Permutations
2.
Are there enough possible passwords for 20 students?
3.
What is the total number of passwords that Ms. Jones can
create?
Activity 4: Permutations
4.
Discussion: Explain how to find the number of passwords
possible if there are 5 letters available, A, B, C, D, and E.
Permutation
• Order matters !!!
– The passwords ABCD and ABDC are different
because order matters
– If the order is of significance, the multiplication
rules are often used when several choices are
made from one and the same set of objects.
Permutations- Definition
• In general, if r objects are selected from a set of
n objects, any particular arrangement of these r
objects (say, in a list) is called a permutation.
• In other words, a permutation is an ordered
arrangement of objects.
• By multiple principle, the total number of
permutations of r objects selected from a set of
n objects is n(n-1)(n-2)·…·(n-r+1)
Permutations –More examples
• Examples
– How many permutations of 3 of the first 5
positive integers are there?
– How may permutations of the characters in
COMPUTER are there? How many of these end
in a vowel?
– How many batting orders are possible for a
nine-man baseball team?
Permutations - Calculation
• Background-Factorial notation:
– 1!=1, 2!=(2)(1)=2, 3!=(3)(2)(1)=6
– In general, n!= n(n-1)(n-2) ·…·3·2·1 for any positive
integer n.
– It is customary to let 0!=1 by definition.
• Calculation of Permutation
n Pr  n(n  1)( n  2)   (n  r  1)
n(n  1)( n  2)  (n  r  1)( n  r )!

(n  r )!

n!
( n  r )!
Permutations -- Special Cases
1.
P(n,0)
2.
There’s only one ordered arrangement of zero objects,
the empty set.
n!
P(n,1)
P(n,1) 
n
3.
There are n ordered arrangements of one object.
P(n,n) P(n, n)  n!  n!  n!
P(n,0) 
n!
n!
 1
(n  0)! n!
(n  1)!
(n  n)! 0!
There are n! ordered arrangements of n distinct objects
(multiplication principle)
Combinations
• An NBA team has 12 players, in how ways
we can choose 5 from 12?
• Can we use permutations?
• Are we interested in the order of the
players?
Combinations (cont.)
• A combination is the same as a subset.
• When we ask for the number of
combinations of r objects chosen from a set
of n objects, we are simply asking “How
many different subsets of r objects can be
chosen from a set of n objects?”
• The order does not matter.
Combinations (cont.)
• Any r objects can be arranged among
themselves in r! permutations, which only
count as one combination.
• So the n(n-1)(n-2)…(n-r+1) different
permutations of r objects chosen from a set
of n objects contain each combination r!
times.
Combinations -- Definition
The number of combinations of r objects
chosen from a set of n objects is:
for r=0,1,2,…,n
Or
n(n  1)( n  2)   (n  r  1)
r!
n!
(n  r )! r!
Other notations for C(n,r) are:
n
n Cr , C , 
 r 
 
n
r
Combinations (cont.)
• For each combination, there are r! ways to
permute the r chosen objects.
• Using the multiplication principle:
C(n,r)r!=P(n,r)
(Number of ways to
choose the objects)
n
 
r
*
(Number of ways to arrange
the objects chosen)
are refer as binomial coefficients
Combinations –More examples
In how many ways a committee of five can be selected from
among the 80 employees of a company?
 80  80  79  78  77  76
  
 24,040,016
5!
5
In how many ways a research worker can choose eight of the
12 largest cities in the United States to be included in a
survey?
12  12! 479,001,600
  

 495
 8  4!8! 24  40,320
Combinations (cont.)
Lets introduce a simplification:
n  n 
   

r  n  r
When we choose r objects from a set of n objects we leave
(n-r) of the n objects, so there are as many ways of leaving
(or choosing) (n-r) objects as there are of choosing r
objects.
So for the solution of the previous problem, we have:
12  12  12 1110  9
     
 495
8
4
4
!
   
Combinations -- Special Cases
• C(n,0):
n!
C (n,0) 
1
0!(n  0)!
• C(n,1):
C (n,1) 
• C(n,n):
n!
C (n,0) 
1
n!(n  n)!
n!
n
1!(n  1)!
there is only one way to
chose 0 objects from the
n objects
there are n ways to select
1 object from n objects
there is only one way to
select n objects from n
objects, and that is to
choose all the objects
Permutations or Combinations ?
• There are fewer ways in a combinations problem than a
permutations problem.
• The distinction between permutations and combinations
lies in whether the objects are to be merely selected or
both selected and ordered. If ordering is important, the
problem involves permutations; if ordering is not
important the problem involves combinations.
Permutations or Combinations ?
• C(n,r) can be used in conjunction with the multiplication
principle or the addition principle.
• Thinking of a sequence of subtasks may seem to imply
ordering bit it just sets up the levels of the decision tree,
the basis of the multiplication principle.
• Check the Fig 3. 9 to get an idea about the difference
between permutation and combination.
Eliminating duplicate
• A committee of 8 students is to be selected from a
class consisting of 19 freshmen and 34
sophomores. In how many ways can a committee
with at least 1 freshman be selected?
Eliminating duplicate
• How many distinct permutations are there of the
characters in the word Mongooses?
• How many distinct permutations are there of the
characters in the word APALACHICOLA?
Eliminating duplicate (cont.)
In general, suppose there are n objects of which a
set of n1 are indistinguishable for each other,
another set of n2 are indistinguishable from each
other, and so on, down to nk objects that are
indistinguishable from each other. The number
of distinct permutations of the n objects is
n!
(n1!)( n 2!)..........(nk!)
Combinations with Repetitions
• A jeweler designing a pin has decided to use two
stones chosen from diamonds, rubies and
emeralds. In how many ways can the stones be
selected?
– Answer-- {D,R}, {D,D}, {D,E}, {E,R},{E,E}, {R,R}.
• Any other way to solve this problem? What if he
needs five stones?
Combinations with Repetitions (cont.)
• Some hints?
–
–
–
–
1 diamond, 3 rubies and 1 emerald
5 diamond, 0 rubies and 0 emerald
0 diamond, 5 rubies and 0 emerald
0 diamond, 0 rubies and 5 emerald
What is it? Choose 5 stars from 7 elements,
i.e.C(7,5)
Combinations with Repetitions (cont.)
• In general, there must be n-1 markers to indicate the
number of copies of each of the n objects.
• We will have r + (n-1) slots to fill (objects + markers).
• We want the number of ways to select r out of the
previous slots to fill.
• Therefore we want:
(r  n  1)!
(r  n  1)!
C (r  n  1, r ) 

r!(r  n  1  r )! r!(n  1)!
• Six children use one lollipop each from a selection of red,
yellow, and green lollipops. In how many ways can this be
done?
Activity 4: Find a Sample Space
• The set of all possible outcomes of a probability experiment
is called the sample space. The sample space may be quite
small, as it is when you toss a coin (sample space: heads or
tails).
•
Situation: A number cube is numbered from 1 to 6. A
spinner has 5 equal sections lettered from A through E. You
can use an organized list to find the sample space for an
experiment.
How can you tell which is experimental and which is
theoretical probability?
Experimental:
Theoretical:
You tossed a coin 10
Toss a coin and getting a
times and recorded a
head or a tail is 1/2.
head 3 times, a tail 7
P(head) = 1/2
times
P(tail) = 1/2
P(head)= 3/10
• You don’t actually do
P(tail) = 7/10
the task
• You actually perform
the task
Experimental probability
Experimental probability is found by
repeating an experiment and observing the
outcomes.
P(head)= 3/10
A head shows up 3 times out of 10 trials,
P(tail) = 7/10
A tail shows up 7 times out of 10 trials
Compare experimental and
theoretical probability
Both probabilities are ratios that
compare the number of favorable
outcomes to the total number of
possible outcomes
P(head)= 3/10
P(tail) = 7/10
P(head) = 1/2
P(tail) = 1/2
Contrast Experimental and theoretical probability
Experimental Vs. Theoretical
0.7
0.6
0.5
Lisa
0.4
Tom
0.3
Al
0.2
0.1
0
Exp P(H)
P(H)
Exp P(T)
P(T)
Identifying the Type of Probability
• A bag contains three
red marbles and three
blue marbles.
P(red) = 3/6 =1/2
 Theoretical
(The result is based on the
possible outcomes)
Identifying the Type of Probability
Trial
Red
Blue
1
2
1
1
3
4
1
1
5
1
6
1
Total
Exp. Prob.
2
4
1/3
2/3
• You draw a marble out of
the bag, record the color,
and replace the marble.
After 6 draws, you record 2
red marbles
P(red)= 2/6 = 1/3
 Experimental
(The result is found by
repeating an experiment.)
How come I never get a theoretical value in both
experiments? Tom asked.
• If you repeat the
experiment many
times, the results will
getting closer to the
theoretical value.
Experimental VS. Theoretical
54
53
52
51
50
49
• Law of the Large
Numbers
53.4
50
49.87
48.4
48
47
46
45
1
48.9
Thoeretical
5-trial
10-trial
20-trial
30-trial
Law of the Large Numbers 101
• The Law of Large Numbers was first published in
1713 by Jocob Bernoulli.
• It is a fundamental concept for probability and
statistic.
• This Law states that as the number of trials
increase, the experimental probability will get
closer and closer to the theoretical probability.
http://en.wikipedia.org/wiki/Law_of_large_numbers
Contrast Experimental and theoretical probability
Three students tossed a coin 50 times individually.
•
•
•
•
Lisa had a head 20 times. ( 20/50 = 0.4)
Tom had a head 26 times. ( 26/50 = 0.52)
Al had a head 28 times. (28/50 = 0.56)
Please compare their results with the theoretical
probability.
• It should be 25 heads. (25/50 = 0.5)
Large Number activity
• Each person is to roll a number cube 20 time
and record their results in the following
table.
Number
rolled
1
2
3
4
5
6
Theoretical
Probability
Frequency
Experimental
Probability
Activity 6: Rock Paper Scissors
• Place the class into groups and use the
activity included.
– Activity PDF
GEOMETRIC PROBABILITY
Some probabilities are found by calculating a ratio of
two lengths, areas, or volumes. Such probabilities are
called geometric probabilities.
Using Area to Find Probability
You throw a dart at the board shown. Your dart is
equally likely to hit any point inside the square board.
Are you more likely to get 10 points or 0 points?
Using Area to Find Probability
Are you more likely to get
10 points or 0 points?
SOLUTION
area of smallest circle
P (10 points) =
area of entire board
2
9  =  ≈ 0.0873

•
3
=
=
182
324
36
area outside largest circle
P (0 points) =
area of entire board
324 – 81
4–
182 – ( • 9 2 )
=
=
=
≈ 0.215
2
18
324
4
You are more likely to get 0 points.
Monte Carlo Area Activity
• Materials
– Blow-up globe.
– Paper and pencil
– Table on slide 75
Monte Carlo Area Activity
• Throw the globe to a participant and have
them catch it with just their finger tips.
• The participant counts how many are
touching land and how many are not.
• Enter the information onto the table on the
next slide
Monte Carlo Area Activity
Trial #
1
2
3
4
5
6
7
8
9
# of fingers
on land for
that trial
Experimental
Probability
Cumulative # of
fingers on land
Cumulative
Experimental
Probability
Monte Carlo Area Activity
• Experimental probability:
• Total surface area of the Earth:
– Approximately 510,065,600 km2
• Multiply the 2 and you should get an
approximation of the surface area of land on
Earth.
– Approximately 148,939,100 km2
Lesson Review
• Probability as a measure of likelihood
• There are two types of probability
• Theoretical--- theoretical measurement and can b
found without experiment
• Experimental--- measurement of a actual
experiment and can be found by recording
experiment outcomes
Please click here to take the quiz
Lesson Review
• 4 ways for counting outcomes
– Making a list
– Tree Diagram
– Combination
– Permutation
• Geometric Probability
Probability Questions
1) Lawrence is the captain of his track team.
The team is deciding on a color and all eight
members wrote their choice down on equal
size cards. If Lawrence picks one card at
random, what is the probability that he will
pick blue?
blue
blue
yellow
green
blue
red
black
black
2) Donald is rolling a number cube labeled 1
to 6. Which of the following is LEAST
LIKELY?
A. an even number
B. an odd number
C. a number greater than 5
1
2
4
3
4
1
2
3. What is the chance of spinning a number
greater than 1?
3
5
4.
5.
What is the chance of spinning a 4?
What is the chance that the spinner will
stop on an odd number?
6. What is the chance of rolling an even number
with one toss of on number cube?