Download PC4.3

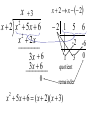
Division and Factors
• When we divide one polynomial by
another, we obtain a quotient and a
remainder. If the remainder is 0, then the
divisor is a factor of the dividend.
Example: Divide to determine whether
x + 3 and x  1 are factors of
3
2
x  2 x  5 x  4.
Division and Factors continued
• Divide:
x 2  5 x  20
x3
x3  2 x 2  5 x  4
x3  3x 2
5 x 2  5 x
5 x 2  15 x
20 x  4
20 x  60
64  remainder
Since the remainder is –64, we know that x + 3
is not a factor.
Division and Factors continued
• Divide:
x2 
x 1
x 4
x3  2 x 2  5 x  4
x3  x 2
 x2  5x
 x2  x
4x  4
4x  4
0  remainder
Since the remainder is 0, we know that x  1 is
a factor.
How do you divide a polynomial by
another polynomial?
• Perform long division, as you do with
numbers! Remember, division is repeated
subtraction, so each time you have a new
term, you must SUBTRACT it from the
previous term.
• Work from left to right, starting with the
highest degree term.
• Just as with numbers, there may be a
remainder left. The divisor may not go into
the dividend evenly.
The Remainder Theorem
If a number c is substituted for x in a
polynomial f(x), then the result f(c) is the
remainder that would be obtained by
dividing f(x) by x  c. That is, if
f(x) = (x  c) • Q(x) + R, then f(c) = R.
Synthetic division is a “collapsed” version of
long division; only the coefficients of the
terms are written.
Synthetic division is a quick
form of long division for
polynomials where the divisor
has form x - c. In synthetic
division the variables are not
written, only the essential part
of the long division.
x
x  2  x   2
3
2 1 5 6
x  2 x  5x  6
2
x  2x
-2 -6
_______
1 3 0
3x  6
quotient
3x  6
_______
2
0
remainder
x  5x  6  ( x  2)( x  3)
2
Example
Use synthetic division to find the quotient
and remainder.
5
4
3
2

4
x

x

6
x

2
x
 50   ( x  2)

2 –4
1
6
2
0
50
–8 –14 –16 –28 –56
–4 –7
–8 –14 –28
–6
Note: We must
write a
0 for
the missing
term.
The quotient is – 4x4 – 7x3 – 8x2 – 14x – 28
and the remainder is –6.
Example continued:
written in the form
P ( x)  d ( x)  Q( x)  R( x)
5
4
3
2

4
x

x

6
x

2
x
 50  

 x  2   -4x
4

 7 x  8 x  14 x  28  6
3
2
By the remainder theorem
we know P(2)  6
Example
• Determine whether 4 is a zero of f(x),
where
f(x) = x3  6x2 + 11x  6.
• We use synthetic division and the
remainder theorem to find f(4).
4 1 –6 11 –6
4 –8 12
1 –2 3 6
• Since f(4)  0, the number is not a zero of
f(x).
The Factor Theorem
• For a polynomial f(x),
if
f(c) = 0, then x  c is
a factor of f(x).
Example: Let
f(x) = x3  7x + 6.
Solve the equation
f(x) = 0 given that x =
1 is a zero.
Solution: Since x = 1 is a
zero, divide synthetically by 1.
1 1 0 -7 6
1 1 -6
1 1 -6 0
Since f(1) = 0, we know that
x  1 is one factor and the
quotient x2 + x  6 is another.
So, f(x) = (x  1)(x + 3)(x  2).
For f(x) = 0, x =  3, 1, 2.
Factor Theorem
• f(x) is a polynomial, therefore f(c) = 0 if
and only if x – c is a factor of f(x).
• If we know a factor, we know a zero!
• If we know a zero, we know a factor!
• Definition of Depressed Polynomial
• A Depressed Polynomial is the quotient
that we get when a polynomial is divided
by one of its binomial factors
• Which of the following can be divided by
the binomial factor (x - 1) to give a
depressed polynomial (x - 1)?
Choices:
A. x2 - 2x + 1
B. x2 - 2x - 2
C. x2 - 3x - 3
D. x2 - 2
Using the remainder theorem to
find missing coeffecients…
• Find the value of k
that results in a
remainder of “0”
given…
( x  3x  kx  24)  ( x  3)
3
2