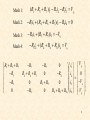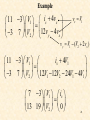* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Mesh Analysis
Mercury-arc valve wikipedia , lookup
Electrical ballast wikipedia , lookup
History of electric power transmission wikipedia , lookup
Three-phase electric power wikipedia , lookup
Signal-flow graph wikipedia , lookup
Mathematics of radio engineering wikipedia , lookup
Electrical substation wikipedia , lookup
Two-port network wikipedia , lookup
Power MOSFET wikipedia , lookup
Switched-mode power supply wikipedia , lookup
Power electronics wikipedia , lookup
Resistive opto-isolator wikipedia , lookup
Voltage optimisation wikipedia , lookup
Buck converter wikipedia , lookup
Topology (electrical circuits) wikipedia , lookup
Surge protector wikipedia , lookup
Current source wikipedia , lookup
Stray voltage wikipedia , lookup
Rectiverter wikipedia , lookup
Opto-isolator wikipedia , lookup
Current mirror wikipedia , lookup
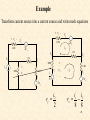
Mains electricity wikipedia , lookup
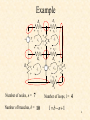
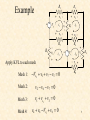
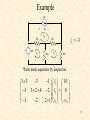
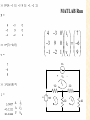
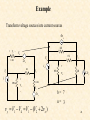
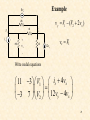
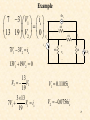
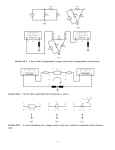
Mesh Analysis Discussion D2.4 Chapter 2 Section 2-8 1 Mesh Analysis • Mesh analysis applies KVL to find unknown currents. • It is only applicable to planar circuits (a circuit that can be drawn on a plane with no branches crossing each other). • A mesh is a loop that does not contain any other loops. • The current through a mesh is known as the mesh current. • Assume for simplicity that the circuit contains only voltage sources. 2 Mesh Analysis Steps 1. Assign mesh currents i1, i2, i3, … il, to the l meshes, 2. Apply KVL to each of the l meshes and use Ohm’s law to express the voltages in terms of the mesh currents, 3. Solve the l resulting simultaneous equations to find the mesh currents. 3 Example R2 R1 + DC Vs2 i1 + R3 - v3 + v2 - v1 - v5 - + v7 - R7 + v6 - R5 i3 + i2 R6 DC Vs1 i4 + v4 - R4 - v + 8 R8 Number of nodes, n = 7 Number of branches, b = 10 Number of loops, l = 4 l b n 1 4 R2 R1 Example DC Vs2 i1 v5 - + R3 Apply KVL to each mesh - v3 + v2 - v1 - + + v7 - R7 + v6 - R5 i3 + Mesh 1: Vs2 v1 v7 v5 0 Mesh 2: v2 v6 v7 0 Mesh 3: v5 vs1 v3 0 Mesh 4: v4 v8 Vs1 v6 0 i2 R6 DC Vs1 i4 + R4 v4 - - v + 8 R8 5 Mesh 1: Vs2 v1 v7 v5 0 Mesh 2: v2 v6 v7 0 Mesh 3: Mesh 4: + DC Vs2 v4 v8 Vs1 v6 0 R3 - v3 + v2 - v1 i1 + v5 vs1 v3 0 Express the voltage in terms of the mesh currents: R2 R1 v5 - + v7 - R7 + v6 - R5 i3 R6 DC + Mesh 1: Vs2 i1 R1 (i1 i2 ) R7 (i1 i3 ) R5 0 Mesh 2: i2 R2 (i2 i4 ) R6 (i2 i1 ) R7 0 Mesh 3: (i3 i1 ) R5 Vs1 i3 R3 0 Mesh 4: i4 R4 i4 R8 Vs1 (i4 i2 ) R6 0 i2 Vs1 i4 + v4 - - v + 8 R8 6 R4 Mesh 1: Vs2 i1 R1 (i1 i2 ) R7 (i1 i3 ) R5 0 Mesh 2: i2 R2 (i2 i4 ) R6 (i2 i1 ) R7 0 Mesh 3: (i3 i1 ) R5 Vs1 i3 R3 0 Mesh 4: i4 R4 i4 R8 Vs1 (i4 i2 ) R6 0 Mesh 1: ( R1 R5 R7 )i1 R7i2 R5i3 Vs2 Mesh 2: R7i1 ( R2 R6 R7 )i2 R6i4 0 Mesh 3: R5i1 ( R3 R5 )i3 Vs1 Mesh 4: R6i2 ( R4 R6 R8 )i4 Vs1 7 Mesh 1: ( R1 R5 R7 )i1 R7i2 R5i3 Vs2 Mesh 2: R7i1 ( R2 R6 R7 )i2 R6i4 0 Mesh 3: R5i1 ( R3 R5 )i3 Vs1 Mesh 4: R1 R5 R7 R7 R5 0 R6i2 ( R4 R6 R8 )i4 Vs1 R7 R2 R6 R7 R5 0 0 R6 R3 R5 0 i1 Vs2 0 i2 i3 Vs1 0 R4 R6 R8 i4 Vs 1 0 R6 8 R1 R5 R7 R7 R5 0 R7 R2 R6 R7 R5 0 0 R6 R3 R5 0 i1 Vs2 0 i2 i3 Vs1 0 R4 R6 R8 i4 Vs 1 0 R6 Ri = v R is an l x l symmetric resistance matrix i is a 1 x l vector of mesh currents v is a vector of voltages representing “known” voltages 9 Writing the Mesh Equations by Inspection R2 R1 + DC Vs2 i1 + R3 - v3 + + v2 - v1 - v5 - + v7 - R7 + v6 - R5 i3 R1 R5 R7 R7 R5 0 i2 R6 DC Vs1 i4 + v4 - R4 R7 R2 R6 R7 R5 0 0 R6 R3 R5 0 i1 Vs2 0 i2 i3 Vs1 0 R4 R6 R8 i4 Vs 1 0 R6 - v + 8 R8 •The matrix R is symmetric, rkj = rjk and all of the off-diagonal terms are negative or zero. The rkk terms are the sum of all resistances in mesh k. The rkj terms are the negative sum of the resistances common to BOTH mesh k and mesh j. The vk (the kth component of the vector v) = the algebraic sum of the independent voltages in mesh k, with voltage rises taken as positive. 10 MATLAB Solution of Mesh Equations R1 R5 R7 R7 R5 0 R7 R2 R6 R7 R5 0 0 R6 R3 R5 0 i1 Vs2 0 i2 i3 Vs1 0 R4 R6 R8 i4 Vs 1 0 R6 Ri = v 1 iR v 11 Test with numbers DC R3 4V 3 R1 R2 2 3 i1 4 i2 R7 1 2 R5 R6 i3 DC 2V i4 4 1 R8 4 1 0 i1 4 2 4 1 4 3 2 4 0 2 i2 0 1 0 3 1 0 i3 2 2 0 2 4 1 i4 2 0 12 R4 Test with numbers 4 1 0 i1 4 2 4 1 4 3 2 4 0 2 i2 0 1 0 3 1 0 i3 2 2 0 2 4 1 i4 2 0 7 4 1 0 i1 4 4 9 0 2 i2 0 1 0 4 0 i3 2 0 2 0 7 i4 2 Ri = v 13 MATLAB Run DC R3 4V 3 R1 R2 2 3 i1 4 i2 R7 1 2 R5 R6 i3 DC 2V i4 4 R4 1 R8 4 1 0 i1 4 2 4 1 4 3 2 4 0 2 i2 0 1 0 3 1 0 i3 2 0 2 0 2 4 1 i4 2 14 PSpice Simulation MATLAB: 15 What happens if we have independent current sources in the circuit? 1. Assume the voltage across each current source is known. 2. Write the mesh equations in the same way we did for circuits with only independent or dependent voltage sources. 3. Express the current of each independent current source in terms of the mesh currents. 4. Rewrite the equations with all unknown mesh currents on the left hand side of the equality and all known voltages on the r.h.s. of the equality. 16 Example 3A + 1 DC 10V i1 va - i3 i3 3 i2 Write mesh equations by inspection. 3 1 i1 10 1 3 3 3 2 4 2 i2 0 1 i v 2 2 1 3 a 17 4 3 1 i1 10 3 9 2 i2 0 1 2 3 3 v a 4 3 0 i1 7 3 9 0 i2 6 1 2 1 v 9 a 18 MATLAB Run 4 3 0 i1 7 3 9 0 i2 6 1 2 1 v 9 a 3A + 1 DC A A V i1 i2 va 10V i1 va - i3 i2 19 PSpice Simulation + - i2 i1 MATLAB: va i1 i2 va 20 Nodal Analysis vs Mesh Analysis • • If the circuit is nonplanar we must use nodal analysis. If the circuit is planar, there are two principle considerations: – – The number of equations we need to write. The information we need in the circuit. For example, do we want to find a current or a voltage? 21 The Number of Mesh Equations If the circuit has only voltage sources or current sources in parallel with resistances (that is, current sources that can be exchanged for voltage sources) then after we have exchanged the current sources, we have to write l mesh equations and the fundamental theorem of network topology tells us that: l b (n 1) 22 The Number of Nodal Equations We also know that if the circuit has only current sources or voltage sources in series with resistances (that is, sources that can be transformed to current sources) then after we have transformed the voltage sources, the number of nodal equations is (n - 1). If we are not interested in the currents through voltage sources or voltages across current sources we may be able to reduce the number of equations we have to write. 23 Example Transform voltage sources into current sources 4vx + vy 2S - V4 + - 2vx is V1 is V2 + 1/8 vx - S V1 V3 + - 3v y v y V1 V4 V1 (V2 2vx ) V2 + 8S vx S 12v y - b= 7 n= 3 24 Example 4vx v y V1 (V2 2vx ) 2S S V1 is V2 + 8S vx S 12v y vx V1 - Write nodal equations 11 3 V1 is 4vx 12v 4v x 3 7 V2 y 25 Example 11 3 V1 is 4vx 12v 4v x 3 7 V2 y vx V1 v y V1 (V2 2vx ) is 4V1 11 3 V1 3 7 V2 12V1 12V2 24V1 4V1 7 3 V1 is 13 19 V2 0 26 Example 4vx 7 3 V1 is 13 19 V2 0 V 2S S 1 7V1 3V2 is 13V1 19V2 0 13 V2 V1 19 3 13 7V1 V1 is 19 is V2 + 8S vx S 12v y - V1 0.1105is V2 0.0756is 27 Example Transform current source into a current source and write mesh equations + + vy - V4 + vx V3 + - is 8 - 2vx V2 + - + V1 V2 + 1/8 1/8 V4 i2 2vx V1 - - is vy V5 + - 3v y i2 vy 2 vx - i1 V3 + - is i1 vx 8 8 28 3v y + Example vy - V4 i2 + 2vx V1 V2 + 1/8 is 8 - V5 + - vx - i1 V3 + - 3v y 1 i1 is 8 3vy 1 8 1 1 4 2v 1 1 2 1 i2 x 29 1.375 1 i1 is 8 3vy 2v 1 1.5 i2 x is i1 vx 8 8 Example i2 vy 2 1.375 1 i1 is 8 1.5i2 0.25i 0.25i 1 1.5 i2 s 1 1.375 0.5 i1 is 8 0.25i 1.25 1.5 i2 s 30 Example 1.375 0.5 i1 is 8 0.25i 1.25 1.5 i2 s + vy - V4 i1 0.1163is i2 is 8 - 2vx V1 V2 + 1/8 i2 0.0698is + V5 + - vx - i1 V3 + - 31 3v y