Download DengNeuroCircuits - UNL Math Department

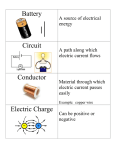
Bo Deng
University of Nebraska-Lincoln
Topics:
 Circuit Basics
 Circuit Models of Neurons
--- FitzHuge-Nagumo Equations
--- Hodgkin-Huxley Model
--- Our Models
 Examples of Dynamics
--- Bursting Spikes
--- Metastability and Plasticity
--- Chaos
--- Signal Transduction
Joint work with undergraduate and graduate students: Suzan Coons, Noah
Weis, Adrienne Amador, Tyler Takeshita, Brittney Hinds, and Kaelly Simpson
Circuit Basics
 Q = Q(t) denotes the net
positive charge at a point
of a circuit.
 I = dQ(t)/dt defines the
current through a point.
 V = V(t) denotes the voltage
across the point.
Analysis Convention: When discussing current, we first assign
a reference direction for the current I of each device. Then we have:
 I > 0 implies Q flows in the reference direction.
 I < 0 implies Q flows opposite the reference direction.
Review of Elementary Components
Capacitors
 A capacitor is a device that stores
energy in an electric potential
field.
Q
Inductors
 An inductor is a device
that stores (kinetic)
energy in a magnetic
field.
dI/dt
Inductor
dI
d 2Q
V L L 2
dt
dt
Resistors
 A resistor is an energy
converting device.
 Two Types:

Linear



Obeying Ohm’s Law: V=RI,
where R is resistance.
Equivalently, I=GV with G =
1/R the conductance.
Variable

Having the IV – characteristic
constrained by an equation
g (V, I )=0.
I
g (V, I )=0
V
Kirchhoff’s Voltage Law
 The directed sum of electrical
potential differences around a
circuit loop is 0.
 To apply this law:
1)
2)
Choose the orientation of the
loop.
Sum the voltages to zero (“+”
if its current is of the same
direction as the orientation
and “-” if current is opposite
the orientation).
Kirchhoff’s Current Law
 The directed sum of the currents
flowing into a point is zero.
 To apply this law:
1)
2)
Choose the directions of the
current branches.
Sum the currents to zero (“+” if a
current points toward the point
and “-” if it points away from the
point).
Example
 By Kirchhoff’s Voltage Law
 with Device Relationships
 and substitution to get
or
Circuit Models of Neurons
I = F(V)
0  C  1
Excitable Membranes
• Kandel, E.R., J.H. Schwartz, and T.M. Jessell
Principles of Neural Science, 3rd ed., Elsevier, 1991.
• Zigmond, M.J., F.E. Bloom, S.C. Landis, J.L. Roberts, and L.R. Squire
Fundamental Neuroscience, Academic Press, 1999.
Neuroscience: 3ed
Hodgkin-Huxley Model
Kirchhoff’s Current Law
- I (t)
-I (t)
(Non-circuit) Models for Excitable Membranes
• Morris, C. and H. Lecar,
Voltage oscillations in the barnacle giant muscle fiber,
Biophysical J., 35(1981), pp.193--213.
• Hindmarsh, J.L. and R.M. Rose,
A model of neuronal bursting using three coupled first order differential
equations,
Proc. R. Soc. Lond. B. 221(1984), pp.87--102.
• Chay, T.R., Y.S. Fan, and Y.S. Lee
Bursting, spiking, chaos, fractals, and universality in biological
rhythms, Int. J. Bif. & Chaos, 5(1995), pp.595--635.
• Izhikevich, E.M
Neural excitability, spiking, and bursting,
Int. J. Bif. & Chaos, 10(2000), pp.1171--1266.
(also see his article in SIAM Review)
Our Circuit Models
Equations for Ion Pumps
 By Ion Pump Characteristics
 with substitution and assumption
 to get
Dynamics of Ion Pump as Battery Charger
Equivalent IV-Characteristics
--- for parallel sodium channels
Passive sodium current can be explicitly expressed as
Equivalent IV-Characteristics
--- for serial potassium channels
Passive potassium current can be implicitly expressed as
0
A standard circuit technique to represent the hysteresis is to
turn it into a singularly perturbed equation
Examples of Dynamics
---------
Bursting Spikes
Metastability & Plasticity
Chaotic Shilnikov Attractor
Signal Transduction
Geometric Method of Singular Perturbation
Small Parameters:
 0 < e << 1 with ideal
hysteresis at e = 0
 both C and l have
independent time scales
Rinzel & Wang (1997)
Bursting Spikes
C = 0.005
Metastability and Plasticity
Terminology:
 A transient state which behaves like a steady state is
referred to as metastable.
 A system which can switch from one metastable state
to another metastable state is referred to as plastic.
Metastability and Plasticity
Neural Chaos
C = 0.005
gNa = 1
dNa = - 1.22
v1 = - 0.8
v2 = - 0.1
ENa = 0.6
gK = 0.1515
dK = -0.1382
i1 = 0.14
i2 = 0.52
EK = - 0.7
C = 0.5
C = 0.5
l = 0.05
g = 0.18
e = 0.0005
Iin = 0
Myelinated Axon with Multiple Nodes
Inside the cell
Outside the cell
Signal Transduction along Axons
Neuroscience: 3ed
Neuroscience: 3ed
Neuroscience: 3ed
Circuit Equations of Individual Node
 dV
C
C I
 I Na  f K VC  EK   I A
ext



dt


  l I S VC  g I A 
I A


V  g I 
I

l
I

 S
A  C
A 


I

e
I

V

E

h


 Na
Na
Na  Na 
C

Coupled Equations for Neighboring Nodes
• Couple the nodes by
adding a linear resistor
between them

1
VC2 VC1
 dVC
 1

1
1
1
 Iext  I Na  f K VC  EK   I A 
C
R1


dt

 1
 dI


 A  l I 1 V 1  g I 1 
S C
A
 dt
 1
 dI S
 l I 1A VC1  g I 1A 



 dt

1
 dI Na
 VC1  E1Na  hNa  I 1Na 
e



dt

 dV 2
VC2 VC1
 2

2
2
2
C
C
  I Na  f K VC  EK   I A 

R1


dt

 dI 2
 A  l I 2 V 2  g I 2 
S  C
A 
 dt

 dI 2
 S  l I 2 V 2  g I 2 
A  C
A 
 dt

 dI 2
Na  V 2  E 2  h  I 2 
e
Na
Na  Na 
C

dt
The General Case for N Nodes
 This is the general
equation for the nth
node
 In and out currents are
derived in a similar
manner:

















dVCn
n1  I n  f V n  E n   I n  I n
C
  Iout
in
Na
K  C
K 
A
dt
dI An
 l I Sn VCn  g I An 


dt
dI Sn
 l I An VCn  g I An 


dt
n
dI
n h In 
e Na  VCn  ENa
Na  Na 
dt
 I
 ext
n

1
Iout  V n V n1
C
 C
n

1

R

 n1
n
VC  VC
Iinn   Rn

0
if n  1
if n  1
if 1  n  N
if n  N
C=.1 pF
(x10 pF)
C=.7 pF
C=.7 pF
Transmission Speed
C=.1 pF
C=.01 pF
Closing Remarks:
 The circuit models can be further improved by dropping the
serial connectivity of the passive electrical and
diffusive currents.
 Existence of chaotic attractors can be rigorously proved,
including junction-fold, Shilnikov, and canard attractors.
 Can be fitted to experimental data.
 Can be used to form neural networks.
References:
 A Conceptual Circuit Model of Neuron, Journal of Integrative
Neuroscience, 2009.
 Metastability and Plasticity of Conceptual Circuit Models of
Neurons, Journal of Integrative Neuroscience, 2010.