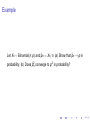Download Converge in probability and almost surely

Converge in probability and
almost surely
Definition: A random sample
The random variables X1 , · · · , Xn are called a random sample
of size n from population f (x) if X1 , · · · , Xn are mutually
independent and each Xi has the same distribution f (x).
Usually X1 , · · · , Xn are called independent and identically
distributed (iid) random variables.
The joint pdf or pmf of X1 , · · · , Xn is given by
f (x1 , · · · , xn ) =
n
Y
i=1
f (xi ).
Example
Suppose X1 , · · · , Xn are observed failure time of n bulbs. We
might assume X1 , · · · , Xn be a random sample from an
exponential(λ) population, where λ is unknown. The joint pdf of
the sample is
f (x1 , x2 , · · · , xn ) = λ
−n
exp(−
n
X
i=1
xi /λ).
Definition: Statistic
I
Let X1 , · · · , Xn be a random sample of size n from a
population and let T (x1 , · · · , xn ) be a real-valued or
vector-valued function. The random variable
Y = T (X1 , · · · , Xn ) is called a statistic, which does not
depend on any unknown parameter. The probability
distribution of a statistic Y is called sampling distribution of
Y.
I
Examples: Let X1 , · · · , Xn be a random sample.
P
1 Pn
¯
X̄n = n1 ni=1 Xi and Sn2 = n−1
i=1 (Xi − Xn ) are the
sample mean and sample variance respectively.
Converge in probability
Definition: Let X1 , · · · , Xn be a sequence of random variables
in probability space (S, F , P). The sequence {Xn } is said to
converge in probability to a random variable X if for any > 0,
lim P(|Xn − X | > ) = 0.
n→∞
Example
Let X1 , · · · , Xn be a sequence of random variables from
Unif(0,1) distribution. Let Mn = max{X1 , · · · , Xn }. Show that Mn
converge to 1 in probability.
Weak law of large numbers
Let X1 , · · · , Xn be iid random variables with mean E(Xi ) = µ
P
and variance Var(Xi ) = σ 2 < ∞. Define X̄n = n1 ni=1 Xi . Then,
for every > 0,
lim P(|X̄n − µ| > ) = 0.
n→∞
That is X̄n converges in probability to µ.
Example: Monte Carlo integration
Suppose we want to evaluate the integral
1
Z
I(h) =
h(x)dx
0
for a complicated function h. If the integration exists and but
hard to calculate, we can use the following approximation:
generating a large number of iid random variables
U1 , U2 , · · · , Un from Unif(0,1) and approximate I(h) by
n
Î(h) =
1X
h(Ui ).
n
i=1
Convergence of function of random variables
Suppose that X1 , X2 , · · · , converges in probability to a random
variable X and h is a continuous function. Then
h(X1 ), h(X2 ), · · · converges in probability to h(X ).
Example
Let Xn ∼ Binomial(n, p) and p̂n = Xn /n. (a) Show that p̂n → p in
probability. (b) Does p̂n2 converge to p2 in probability?
Almost surely convergence
Definition: Let X1 , · · · , Xn be a sequence of random variables
in probability space (S, F , P). The sequence {Xn } is said to
converge almost surely to a random variable X if
P({s : lim Xn (s) = X (s)}) = 1.
n→∞
Example
Let the sample space S be the closed interval [0,1] and P be
the uniform probability measure on [0, 1]. Define Xn (s) = s + sn
and X (s) = s. Does Xn (s) converge to X (s) almost surely?
Example: Converge in probability, but not almost
surely
Let Xn be a sequence of random variables on ([0, 1], F , P) and
P be the uniform probability measure on [0, 1]. Define
Xn (s) = IAn (s)
m
m
where An = [ 2km , k+1
2m ], n = k + 2 , k = 0, · · · , 2 − 1 and
m = 0, 1, 2, · · · . Show that Xn (s) converge to 0 in probability
but not almost surely.
Strong law of large numbers
Let X1 , · · · , Xn be iid random variables with mean E(Xi ) = µ
P
and variance Var(Xi ) = σ 2 < ∞. Define X̄n = n1 ni=1 Xi . Then,
for every > 0,
P( lim |X̄n − µ| > ) = 0.
n→∞
That is X̄n converges almost surely to µ.