Download Chapter 2

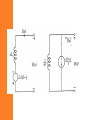
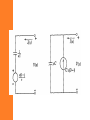
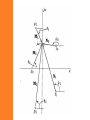
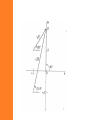
Network Analysis and Synthesis
Chapter 2
Network transform representation
and analysis
2.1 The transformed circuit
• When analyzing a network in time domain we
will be dealing with
– Derivation and
– Integration
• However, when transformed to complex
frequency domain these become
– Derivation -> multiplication by ‘s’
– Integration -> division by ‘s’
• Hence, it is easier to do network analysis in
complex frequency domain.
• The voltage current relationships of network
elements in time domain and complex
frequency domain are given as:
• Resistor
v(t )  Ri (t )
V ( s)  RI ( s )
• Inductor
– The time domain relation ships are
v(t )  L
di (t )
dt
t
1
i (t )   v( )d  i (0  )
L 0
– In frequency domain they become
V ( s )  sLI ( s )  Li (0  )
V ( s ) i (0  )
I ( s) 

sL
s
• An inductor is represented in frequency
domain as
– An impedance sL in series with a voltage source
Used in mesh analysis.
or
– An admittance 1/sL in parallel with a current
source
Used in nodal analysis.
• Capacitor
– The time domain relation ships are
t
1
v(t )   i ( )d  v(0  )
C 0
i (t )  C
dv(t )
dt
– In frequency domain they become
I ( s ) v (0  )
V (s) 

sC
s
I ( s )  sCV ( s )  Cv(0  )
• A capacitor is represented in frequency
domain as
– An impedance 1/sC
source
in series with a voltage
Used in mesh analysis.
or
– An admittance sC in parallel with a current source
Used in nodal analysis.
Example 1
• In the figure below, the switch is switched from
postion 1 to 2 at t=0. Draw its transformed circuit and
write the transformed equations using mesh analysis.
• The transformed circuit is
• The transformed equations become
Example 2
• The switch is thrown to position 2 at t=0. Find
i(t). i (0 )  2amp

L
vC (0 )  2V
• The transformed circuit is
• Writing the transformed equation
5
2 
2
 2    3  s   I ( s)
s
s 
s
• Solving for I(s)
2s  3
( s  2)( s  1)
1
1
I (s) 

s  2 s 1
I (s) 
• Inverse transforming
i(t )  e
2t
e
t
Example 3
• At t=0, the switch is opened. Find the node
voltages v1 and v2
1
h
2
G  1 mho
L
C  1f
V  1v
• The transformed circuit becomes
• The transformed equations become
• Solving these 2 equations
2.2 System function
• The excitation , e(t), and response, r(t), of a linear
system are related by a linear differential equation.
• When transformed to complex frequency domain the
relationship between excitation and response is
algebraic one.
• When the system is initially inert, the excitation and
response are related by the system function H(s)
given by
R( s)  H ( s) E ( s)
• The system function may have many different
forms and may have special names. Such as:
– Driving point admittance
– Transfer impedance
– Voltage or current ratio transfer function
• This is because the excitation and response
may be taken from the same port or different
ports and the excitation and response can be
either voltage or current.
Impedance
• Transfer impedance is when the excitation is a
current source and the response is a voltage.
V0 ( s)
H ( s) 
I g ( s)
• When both the excitation and response is at
the same port it is called driving point
impedance.
1
sL
H ( s )  R  sC
1
 sL
sC
Admittance
• Transfer admittance is when the excitation is a
voltage source and the response is a current.
I 0 ( s)
H ( s) 
Vg (s)
1
H (s) 
1
sL 
R
sC
Voltage ratio transfer function
• When the excitation is a voltage source and
the response is a voltage.
V0 (s)
H ( s) 
Vg (s)
Z 2 ( s)
H ( s) 
Z1 ( s)  Z 2 ( s)
Current ratio transfer function
• When the excitation is a current source and
the response is a current.
I 0 ( s)
H ( s) 
I g ( s)
1
H ( s )  sL  R
1
sC 
sL  R
1
sC
H (s) 
1
R  sL 
sC
• Note that, the system function is a function of
the system elements only.
• It is obtained from the network by using the
standard circuit laws. Such as:
– Kirchhoffs law
– Nodal analysis
– Mesh analysis
Example 4
• Obtain the driving point impedance of the network.
Then using the following excitations determine the
response.
1. ig (t )  Sinwot u (t )
2. The square pulse on figure b
3. The waveform on figure c
a
b
c
• First lets find the driving point impedance
• Note that it is the equivalent impedance of
the 3 elements
1
s
H ( s) 

1
sC   G C  s 2   G  s  1 
sL
 C  CL 

1. ig (t )  Sinwot u (t )
Its transform is
w0
I (S )  2
s  wo2
Hence, the response is
wo
s
Vo ( s )  I g ( s ) H ( s )  2
.
2
G
1 
s  wo  2
C s  s 
C LC 

2. The excitation is given as
i (t )  u (t )  u (t  a )
1 1  as
I (s)   e
s s
Hence, the response is
1 e
Vo ( s)  I g ( s) H ( s) 
s
 as
s
.
G 1 
 2
C s  s 
C LC 

3. The excitation is given as
t
t a
ig (t )  u (t )  u (t ) 
u (t  a)
a
a
1 1 e  as
I (s)   2  2
s as
as
• Consider the partial fraction expansion of R(s)
where si are the poles of H(s) and sj are the poles of E(s).
• Taking the inverse Laplace transform of R(s)
si t
• The terms Ai e are associated with the system
H(s) and are called the free response terms.
s jt
• The terms B j e are due to the excitation E(s)
and are called the forced response terms.
• The frequencies si are the natural frequency of
the system, while the frequencies sj are the
frequencies of the excitation.
Problem
• Find the free response and the forced
response for the circuit below. The system is
inert before applying the source.
1
v g (t )  (cos t )u (t )
2
2.3 Poles and zeros of system
• We will discuss the relationship between the
poles and zeros of a system function and its
steady state sinusoidal response.
• In other words, we will investigate the effect
of positions of poles and zeros upon H(s) on
the jw axis.
• To find the steady-state sinusoidal response of
a system function we replace ‘s’ by ‘jw’.
• Hence, the system function becomes
H ( jw)  H ( s) |s  jw
H ( jw)  M ( w)e j ( w)
Where
 M(w) is the amplitude or magnitude response
 φ(w) is the phase response
• The amplitude and phase response of a
system provide valuable information in the
analysis and design of transmission circuits.
• Consider the low pass filter
• Observe that
– It passes only frequency
below wc
– The phase response is
almost linear till wc
• Hence, if all the significant harmonic terms are
less than wc , then the system will produce
minimum phase distortion.
• In the rest of this section, we will concentrate
on methods to obtain amplitude and phase
response curves.
R-C network
•
1
sC
1
V ( s)
H ( s)  2

 RC
1
V1 ( s ) R  1
s
sC
RC
• To obtain H(jw) we substitute s by jw.
H ( jw) 
1
RC
1
jw 
RC
• In polar form H(jw) becomes
1
RC
H ( jw) 
1 
 2
w  2 2 
RC 

M ( w) 
1
RC
1 
 2
w


2 2 
R
C 

 ( w)   tan 1 wRC 
1
2
1
2
e
 j tan 1 wRC
 M ( w)e j ( w )
• The amplitude is unity and the phase is zero
degrees at w=0.
• The amplitude and phase decrease
monotonically as we increase w.
• When w=1/RC, the amplitude is 0.707 and
phase is -450.
Half power point
• As w increases to infinity M(w) goes to zero
and the phase approaches -900.
Amplitude and phase from pole-zero
diagram
• For the system function
H ( s) 
A0 ( s  z0 )( s  z1 )
( s  p0 )( s  p1 )( s  p2 )
• H(jw) can be written as
A0 ( jw  z0 )( jw  z1 )
H ( jw) 
( jw  p0 )( jw  p1 )( jw  p2 )
• Each one of the ( jw  zi ) or ( jw  p j ) represent
a vector from zi or pj to the jw axis at w.
• If we express
j i
jw  zi  Ni e ,
jw  p j  M j e
j j
• Then H(jw) can be given as
A0 N1 N 2 j  0  1  2 0 1 2 
H ( jw) 
e
M 0 M 1M 2
• In general,
Example
4s
F ( s)  2
s  2s  2
• For
phase for w=2.
• Solution
find the magnitude and
– First let us find the zeros and poles
4 jw
F ( jw) 
( jw  1  j )( jw  1  j )
– Zero at jw=0
– Poles at ( jw  1  j )
and
( jw  1  j )
• Magnitude
2
4
M ( j 2)  4 *

2 * 10
5
• Phase
 ( j 2)  900  71.80  450  26.80
Exercise
• Examine the property of F(s) around the poles
and zeroes.
Bode plots
• In this section we turn our attention to semi
logarithmic plots of system function, called
Bode plots.
• In these plots we take the logarithm of the
amplitude and plot it on linear frequency
scale.
• For amplitude M(jw), if we express in terms of
decibel it becomes 20 log M ( jw)
• For system function
H ( s) 
N ( s)
D( s )
M ( jw) | H ( jw) |
| N ( jw) |
| D( jw) |
• If we express the amplitude in terms of
decibels we have
20 log M ( jw)  20 log | N ( jw) | 20 log | D( jw) |
• In factored from both N(s) and D(s) are made up
of 4 kinds of terms
1.
2.
3.
4.
•
•
Constant K
A root at origin, s
A simple real root, s-a
A complex set of roots,
s 2  2s   2   2
To understand the nature of log-amplitude plots,
we only need to discuss the amplitude response
of these 4 terms.
If the term is on the numerator it carries positive
sign, if on denominator negative sign.
1. Constant K
• The dB gain or loss is
20 log K  K2
• K2 is either positive |K|>1 or negative |K|<1.
• The phase is either 00 for K>0, or 1800 for K<0.
Single root at origin, s
• The loss or gain of a single root at origin is
 20 log | jw | 20 log w
• Thus the plot of magnitude in dB vs frequency
is a straight line with slope of 20 or -20.
• 20 when s is in the numerator.
• -20 when s is in the denominator.
• The phase is either 900 or -900.
• 900 when s is in the numerator.
• -900 when s is in the denominator.
The factor s+α
• For convenience lets set α=1. Then the
magnitude is
 20 log | jw  1 | 20 log w  1
2
1
2
• The phase is
arg( jw  1)  tan 1 w
• A straight line approximation can be obtained
by examining the asymptotic behavior of the
factor jw+1.
• For w<<1, the low frequency asymptote is
 20 log w  1  20 log 1  0dB
1
2
2
• For w>>1, the high frequency asymptote is
 20 log w  1  20 log w
2
1
2
Which has a slope of  20 log w decibel/de cade
• These 2 asymptotic approximations meet at w=1.
• Note that the maximum error is for w=1 or
for the non normalized one w=α.
• For the general case α different from 1, we
normalize the term by dividing by α.
• The low frequency asymptote is
1
2
w

20 log  2  1  20 log 1  0dB


2
• The high frequency asymptote is
1
2
w

20 log  2  1  20 log w  20 log 


2
For complex conjugates
• For complex conjugates it is convenient to
adopt a standard symbol.
• We describe the pole (zero) in terms of
magnitude ω0 and angle θ measured from the
negative real axis.
• These parameters that describe the pole
(zero) are ω0, the undamped frequency of
oscillation, and ζ, the damping factor.
• If the pole (zero) pair is given as
p1, 2    j
• α and β are related to ω0 and ζ with
  0 cos   0
  0 sin   0 1   2
• Substituting these terms in the conjugate
equation (s  p1 )(s  p2 )


( jw    j )( jw    j )  jw  0  j0 1   2 jw  0  j0 1   2

  w2  2 jw0  0
2


• For ω0=1 (for convenience), the magnitude of
conjugate pairs can be expressed as

 20 log 1  w2  j 2w  20 log 1  w
• The phase is
 ( w)  tan 1
2 2
1  w2

2 2
 4 2 w

1
2 2
• The asymptotic behavior is
– For low frequency, w<<1

 20 log 1  w

2 2
 4 2 w
  20 log 1  0dB
1
2 2
– For high frequency, w>>1

 20 log 1  w

2 2
 4 2 w
  40 log w
1
2 2
which is a straight line with slope of 40dB/decade.
• These 2 asymptotes meet at w=1.
Example
• Using Bode plot asymptotes, draw the
magnitude vs. frequency for the following
system function
0.1s
G ( s) 
2

s
 s
 s
 3  1
  1
4
 50  16 *10 10

Actual plot