Download 5.3 Use Angle Bisectors of Triangles Theorem 5.5

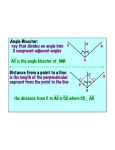
5.3
Use Angle Bisectors of Triangles
Theorem 5.5: Angle Bisector Theorem
If a point is on the bisector of an
angle, then it is equidistant from
the two _______
sides of the angle. A
If AD bisects BAC and DB  AB
and DC  AC, then DB  _____.
DC
B
D
C
5.3
Use Angle Bisectors of Triangles
Theorem 5.6: Converse of the Angle Bisector Theorem
If a point is in the interior of an
angle and is equidistant from the
sides of the angle, then it lies on
A
the _________
bisector of the angle.
If DB  AB and DC  AC and
DB  DC, then AD _______
bisects BAC.
B
D
C
5.3
Use Angle Bisectors of Triangles
Example 1 Use the Angle Bisector Theorem
Find the measure of CBE.
Solution
Because EC  ____,
BD and
BC ED  _____,
EC = ED = 21, BE bisects CBD by
Converse of the Angle Bisector
the ____________________________
Theorem
_________.
21 E
C
21
31
B
DBE  ____.
31
So, mCBE  m_____
o
o
D
5.3
Use Angle Bisectors of Triangles
Example 2 Solve a real-world problem
Web A spider’s position on its web
relative to an approaching fly and the
opposite sides of the web form congruent
angles, as shown. Will the spider have to
move farther to reach a fly toward the
right edge or the left edge?
Solution
The congruent angles tell you that the spider is
bisector of LFR.
on the _________
Angle Bisector Theorem
By the _________________________,
the spider
is equidistant from FL and FR.
same distance to
So, the spider must move the ____________
reach each edge.
L
R
F
5.3
Use Angle Bisectors of Triangles
Example 3 Use algebra to solve a problem
For what value of x does P lie on the bisector of
J?
Solution
From the Converse of the Angle Bisector
x +11
x
K
Theorem, you know that P lies on the
P
bisector of J if P is equidistant from
PL
the sides of J, so then _____
PK = _____.
22xx–5 5
Set segment J
_____
=
_____
PK PL
lengths equal.
L
______ = _______
Substitute expressions for
segment lengths.
______ = _______
Solve for x.
1
x 5
__
6 x
Point P lies on the bisector of J when x = ____.
6
5.3
Use Angle Bisectors of Triangles
Theorem 5.7: Concurrency of Angle Bisector of a Theorem
The angle bisector of a triangle
intersect at a point that is
equidistant from the sides of
the triangle.
A
If AP, BP, and CP are angle
bisectors of ABC, then
PE  ____.
PD  ____
PF
B
D
E
P
F
C
5.3
Use Angle Bisectors of Triangles
Example 4 Use the concurrency of angle bisectors
In the diagram, L is the incenter
of FHJ. Find LK.
By the Concurrency of Angle Bisectors
of a Triangle Theorem, the incenter L
equidistant from the sides of  FHJ.
is __________
So to find LK, you can find ___
LI in  LHI.
Use the Pythagorean Theorem.
2
2
2
___
=
________
c a b
2
2
2
___
=
________
15 LI  12
2
___
LI
81 = ____
___
LI
9 = ____
F
Because ____
9
LI = LK, LK = _____.
15
H
12
G
I
L
J
K
Pythagorean
Theorem
Substitute
known values.
Simplify.
Solve.
5.3
Use Angle Bisectors of Triangles
Checkpoint. In Exercise 1 and 2, find the value x.
1.
xo
25o
Because the segments opposite the angles
are perpendicular and congruent,
by the Converse of the Angle Bisector
Theorem, the ray bisects the angle.
So, the angles are congruent, and x  25
5.3
Use Angle Bisectors of Triangles
Checkpoint. In Exercise 1 and 2, find the value x.
2.
7x + 3
8x
7 x  3  8x
3 x
By the Angle Bisector Theorem, the two
segments are congruent.
5.3
Use Angle Bisectors of Triangles
Checkpoint. In Exercise 1 and 2, find the value x.
3. Do you have enough information to
conclude that AC bisects DAB?
B
A
C
D
No, you must know that mABC and mADC are equal 90o.
5.3
Use Angle Bisectors of Triangles
Checkpoint. In Exercise 1 and 2, find the value x.
3. In example 4, suppose you are not given HL or
HI, but you are given that JL = 25 and JI = 20.
Find LK.
a b  c
2
2
2
LI  20  25
2
LI  400  625
2
LI  225
LI  15
LK  15
2
2
15
2
H
12
G
I
L
K
F
20
J
25
5.3
Use Angle Bisectors of Triangles
Pg. 289, 5.3 #1-12