Download r 0

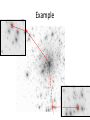
Atmospheric turbulence
Eric Gendron
Wavefront, and image
• The energy (= light rays) propagates orthogonally to the
wavefront
spherical
wavefront
convergence point
=
centre of the sphere
no real convergence
point
non spheric
wavefront
Aberrations
• Difference between the actual wavefront, and the ideal one
• Optical path difference varying across the pupil : d(x,y)
x
d(x,y)
no real convergence
point
aberrated
wavefront
Aberrations : examples
• Astigmatism
convergence point
(center of curvature)
in a vertical plane
convergence point
(center of curvature)
in a horizontal plane
• d(x,y) = x2-y2 or d(x,y) = xy
• Easily created by tilting
a lens in an optical system
Aberrations : examples
• Spherical
rays from pupil edge
converge here
rays from pupil centre
converge here
• wavefront curvature changes linearly with pupil radius
• d(x,y) = r3
• Any simple lens creates spherical aberration
Aberrations : examples
• Defocus
convergence point
(center of curvature)
where convergence
point was expected
• « wrong radius »
• d(x,y) = x2+y2
• Easily created by moving a lens along the optical axis
Aberrations : examples
• Tilt
convergence point
(center of curvature)
where convergence
point was expected
• « image is not centered »
• d(x,y) = x or d(x,y) = y
• Easily created by moving a lens transversal to the optical axis
When aberrations depend on l
• Chromatic
blue wave
converge here
red wave
converge here
• Chromatic aberration of a single lens
– mainly defocus (focal length is shorter at short l)
• In general : wavefront shape depends on wavelength !
– can be anything : spherical in the red, and astigm in the blue
When aberrations depend on field
position
• Field curvature
– defocus varies quadratically with field angle
• Distorsion
– tilt is introduced with field angle
Diffraction
•
2
Image = |electric field in focal plane|
• Electric field in focal plane =
F ( electric field in pupil plane )
• Phase :
 (x, y) 
2
l
d (x, y)
• Electric field in the pupil :

amplitude
A(x, y) exp
i ( x,y )
phase
Diffraction limit
• For a « perfect » wavefront : the image is determined only by
the pupil function of the instrument (assuming uniform
amplitude)
|F [A(x,y)] |2
Diffraction limit
• For a circular aperture : Airy pattern
2
2J1 () 
I( )  

  
l
D
 R
lf
angle 
distance R in
the focal plane

normalized intensity


D

FWHM 
l
D
0 = 1.22 l/D
R0 = 1.22 lf/D

(or R)
Aberrations
• With f(x,y)≠0
– image becomes wider than l/D, light is spread around
– peak intensity is reduced
• Relation between image quality and phase ?
• How to measure image quality ?
Image formation depends on l
F
• Image(u,v) = |
2id (x,y )
[
A(x, y) e
l
] |2
• Same wavefront d(x,y), but different images :

l=1 µm
l=0.7 µm
l=0.5 µm
Phase variance
• The phase variance tells how degraded the wavefront is
:
1
2
2
s 

S pupil
 (x, y) dx dy
• sf2=0 when the wavefront has no aberration
• units : radians2
• proportional
to l-2

f(x,y)
2
l 
s 2 (l1)  s 2 (l 2 ) 2 
l1 
s2 (l1) l12  s 2 (l 2 ) l22  constant
• will allow us to transform quantities in terms of
wavelength

x
Strehl ratio
• Ratio between
– the intensity of the degraded image on the optical axis
– the intensity of the diffraction-limited image on the optical
axis
0 ≤ SR ≤ 1
SR>1 impossible !!!
Idiff
Ideg
SR 
Idiff
Ideg
Phase variance and SR
•
•
•
•
Approximation :
SR  e
Usually ≈ok for sf2< 1 rd2
True when phase is a white noise
Exercice :

s 2
– SR(0.5µm) = 0.40. Determine SR at 1.65 µm.
Atmospheric turbulence
• Turbulence is not sufficient to produce wavefront distorsion
– wavefront is distorted because of random refractive index fluctuations
• Temperature fluctuations are required (and/or water vapor
concentration fluctuations)
cold air
warm air
Atmospheric turbulence
• Air refractive index depends on wavelength
• Air refractive index depends on temperature
air refractive index
0°C
20°C
wavelength
• optical path fluctuations are, at first order, independent of
wavelength : wavefront shape d(x,y) is close to achromatic
Atmospheric turbulence
• Turbulent temperature mixing occurs mainly
– close to the ground (0-40m)
– at inversion layer (1-2 km)
– at jet-stream level (8-12 km)
• Most of it occurs at interface between air slabs
– notion of « turbulent layers »
Atmospheric turbulence
• Fractal properties
• Change of spatial scale turns into amplitude factor
• comes from Kolmogorov statistics (1941) :
– statistical scale invariance of the cascade : sc aling arguments and
dimensional analysis
– ,b?
V = speed
e = energy
V  e Lb
V  e1/ 3 L1/ 3
L = distance
Atmospheric turbulence
• 3-D phase structure function of refractive index :
(n(x)  n(x  r))
2
• True for
l0 < r < L 0
 Dn (r)  CN2 r 2 / 3
: the inertial regime
– inner scale l0
– outer scale L0
• CN2 is called refractive index structure constant
– depends on altitude h : CN2(h)
– is expressed in m-2/3
• Phase variance will vary proportionally to CN2(h)
Atmospheric turbulence
• 3-D phase structure function of refractive index :
(n(x)  n(x  r))
2
• True for
l0 < r < L0
 Dn (r)  CN2 r 2 / 3
: the inertial regime
– inner scale l0
– outer scale L0

• CN2 is called refractive index structure constant
– depends on altitude h : CN2(h)
– is expressed in m-2/3
kolmogorov
L0=100m
• 3D power spectrum :
0.033CN2
W (k) 
k11/ 3
W (k) 
0.033CN2
(k
2
)
2 11/ 6
0
L
Von Karman version
Von Karman
L0=10m
Wavefront statistics
• 2D phase power spectrum : Wiener spectrum
Wf (k) 
0.023
r05 / 3 k11/ 3
• 2D phase structure function

 (x)   (x  r)
(
)
2
5/3
 r 
 D (r)  6.88 
r0 
• r0 characterizes the amplitude of wavefront disturbance

The Fried parameter
• Fried, JOSA, 1966 :
• r0 is the diameter of a diffraction-limited telescope having the same
resolution as an infinitely large telescope limited by the atmosphere
turbulence
large telescope,
limited by the atmosphere
diameter r0
same
resolution
l/r0
image width
The Fried parameter
seeing-limited telescope
diffraction-limited telescope
l/r0
l/D
r0
• When D<r0 : the telescope is limited by diffraction
– wavefront is « nearly flat » over the aperture
• When D>r0 : the telescope is seeing-limited
• r0 : area over which the wavefront can be considered
as « flat »
– with respect to l !
telescope diameter
D
Order of magnitude of r0 ??...
In the visible
Exceptionally :
Astronomical site :
Meudon :
Horizontal propag :
25 cm
10 cm
3 cm
~ mm
The Fried parameter
•
Expression of r0 :
•
Notice that
•

For a fully developped Kolmogorov turbulence :
3 / 5
2


2  1
2
r0  0.423
CN (h) 



l cos


r0  l6 / 5
5/3

D
2
s   1.03  
r0 
– sounds like a definition : r0 =area over which phase variance ≈ 1 rd2
•
Seeing :

seeing  0.976
l
r0
seeing 
l
r0
seeing  l1/ 5
Image properties
• typical atmospheric-degraded image :
– structure with speckles (short exposures)
• Typ. size of a speckle
– l/D
• Typ. size of long exposure image
– l/r0
seeing = l/r0
l/D
Long-exposure
optical transfer function
• One demonstrate that the long-exposure transfer function is
the product between
– the OTF of the telescope
– an OTF specific to atmosphere
H(u)  H tel (u) e
1
 D (u)
2
H(u)

spatial frequency u
r0/l
D/l
Exercice
• On a 1m telescope, seeing is 3 arcsec at lvis=0.5µm.
SR at l=10 µm ?
•
•
•
•
3 arcsec = 1.45e-5 rd =lvis/r0 : r0(0.5µm)=3.4cm
sf2=1.03(D/r0)5/3 = 283 rd2 at lvis=0.5µm
sf2(0.5µm) 0.52 = sf2(10µm) 102 => sf2(10µm) = 0.71 rd2
SR = exp(-0.71) = 0.49
•
or ... scale r0
– r0(10µm) = r0(0.5µm) (10/0.5)6/5 = 1.25m
– sf2(10µm) = 1.03(D/r0)5/3 = 0.71 rd2
Temporal evolution
• One assumes that the layers move as a whole, with speed of
inner eddies slower than the global motion
(Taylor hypothesis)
• One define a correlation time :
– V is the average speed
3/5
 CN2 (h)v(h) 5 / 3 dh 


V  
2
C


N
  (h) dh

• t0 is proportional to l6/5

t 0  0.31
r0
V
Angular anisoplanatism
• isoplanatic : when wavefronts are
the same for the different directions
in the field
• If separated enough, 2 points of the
field will see different wavefronts
directn 1
directn 2
r
• One defines q0  0.31 0
H is the average height H
hB
3/5
 CN2 (h) h 5 / 3 dh 


H  
2
 
  CN (h) dh 

hA
• q0 is proportional to l6/5

telescope pupil
Example
Modal decomposition of phase
• f(x,y,t) not easy to handle
• Decomposition on a modal basis

 (x, y,t)   ai (t) Z i (x, y)
i1
• Zernike modes
–
–
–
–
–
–
–
defined on a circular aperture

analytic expression
1
orthogonal basis
 Z i (x, y) Z j (x, y) dx dy  d ij
S pupil
look like first order optical aberrations
derivatives can be expressed as a simple combination of themselves
Fourier transform has analytic expression

coefficient ai
1
ai 
 Zi (x, y) (x, y) dx dy
S pupil
Zernike modes
m=0
m=1
n=1
n=2
m=2
• Index i refers to n and m, radial and azimutal
orders of the polynomial
• i is increasing with n and m, i.e. with spatial
frequency
m  0 Z i even (r,q )  2(n  1) Rnm (r) cos(mq )
m  0 Z i odd (r,q )  2(n  1) Rnm (r) sin( mq )
m  0 Z i (r,q )  n  1 Rn0 (r)
R (r) 
m
n
(n m )/ 2

s0

1s (n  s)!
r n 2s
s! ((n  m) /2  s)! ((n  m) /2  s)!
Modal decomposition of phase
• Phase variance

s    ai2
2
i1
• Setting one of the ai=0
– best wayto flatten the wavefront
Modal spectrum
• Noll, R.J., JOSA 66, (1976)
tip and tilt
low spatial freq
high spatial freq

 (x, y,t)   ai (t) Z i (x, y)
i1
5/3
D
2
ai  c i  
r0 

Residual error
• Phase error after perfect compensation of J Zernike modes
J 


iJ 1
ai2
5/3
 J  0.257 J
5 / 6
D
 
r0 

• Equivalence Zernike deformable mirror with Na actuators

– Greenwood, JOSA, 69, 1979
5/3
s   0.27 N a
2
5 / 6
D
 
r0 
Residual error
• Re-writing Greenwood formula
5/3
5 / 6 D
2
s   0.27 N a
 
r0 

5/3
D /n a 
2
s   0.335 

r
 0 
na actu across
the diameter
Na 
4
n a2
Na actuators inside the pupil
• sf2 will be kept constant if one keeps product 
(r0 na) constant


Temporal spectrum
log(PSD)
tip-tilt
f-2/3
f0
higher orders
Power Spectral Density
• Temporal spectrum of ai(t)
f-17/3
frequency (hz)
log(f)
fc
f c  0.3(n  1)
V
D
f-11/3
Angular correlations
ai (0) ai (q )
ai2
normalized correlation
tip-tilt
high-order mode

D
(n  1)H
low order mode
separation angle
Thanks for your attention