Download Commutative Property

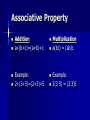
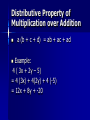
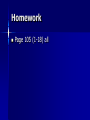
Properties of Algebra
(aka all the rules that holds the
math together!)
Axioms for Rational
Numbers


All of our axioms for rational numbers
are for ONLY addition and
multiplication!!!!
Axiom is just a property that has not
been proven but we accept and use to
do algebra and prove things
Commutative Property



Root word is: commute
To commute means to move
The numbers move places
Commutative Property




Addition:
a+ b = b+a
Example:
2 + 3 = 3 +2

Multiplication

ab= ba


Example:
2(3) = 3(2)
Associative Property




Root word: Associate
To associate means to group together
In math, our grouping symbols are the
()
Keep the order of the numbers the
same!!! Just change the ( )
Associative Property




Addition
a+(b+c)=(a+b)+c
Example:
2+(3+5)=(2+3)+5




Multiplication
a(bc) = (ab)c
Example:
2(3·5) = (2·3)5
Identity Properties




Your identity is who you are
The same goes for numbers and
variables
3 is who 3 is and x is who x is
The idea with the identity property is
you want to get itself back
Identity Property




Addition
a+0=a
Example:
3+0=3




Multiplication
a (1) = a
Example:
3 (1) = 3
Inverse Properties




The inverse in math means the
“opposite”
When we add the opposite of a
positive is a negative and vice versa
When we mult the opposite is the
reciprocal
In an inverse we want our addition to
= 0 and our mult to = 1
Inverse Property




Addition
a + (-a) = 0
Example:
3 + (-3) = 0




Multiplication
a(1/a) =1
Example:
3 (1/3) = 1
Distributive Property



To distribute means to give out
You are giving the # on the outside of
the ( )’s to every # inside the ( )
The distributive property is the only
one that includes addition and mult at
the same time
Distributive Property of
Multiplication over Addition

a (b + c + d) = ab + ac + ad
Example:
4 ( 3x + 2y – 5)
= 4 (3x) + 4(2y) + 4 (-5)
= 12x + 8y + -20

Properties of Equality
Reflexive Property: a =a
Example: 4 =4
 Symmetric Property : If a=b, then b=a
Example: If x= 3, then 3=x
 Transitive Property: If a=b
and b=c
then a=c
Example: If x=3 and 3=y then x=y

Homework

Page 105 (1-18) all