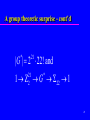Download Tiling - Rose

Tilings, Finite Groups, and
Hyperbolic Geometry at the
Rose-Hulman REU
S. Allen Broughton
Rose-Hulman Institute of Technology
1
Outline






A Philosopy of Undergraduate Research
Tilings: Geometry and Group Theory
Tiling Problems - Student Projects
Example Problem: Divisible Tilings
Some results & back to group theory
Questions
2
A Philosopy of Undergraduate
Research




doable, interesting problems
student - student & student -faculty
collaboration
computer experimentation (Magma, Maple)
student presentations and writing
3
Tilings: Geometry and Group Theory







show ball
tilings: definition by example
tilings: master tile
Euclidean and hyperbolic plane examples
tilings: the tiling group
group relations & Riemann Hurwitz
equations
Tiling theorem
4
Icosahedral-Dodecahedral Tiling
5
(2,4,4) -tiling of the torus
6
Tiling: Definition




Let S be a surface of genus  .
Tiling: Covering by polygons “without
gaps and overlaps”
Kaleidoscopic: Symmetric via reflections
in edges.
Geodesic: Edges in tilings extend to
geodesics in both directions
7
Tiling: The Master Tile - 1
8
Tiling: The Master Tile - 2





maily interested in tilings by triangles and
quadrilaterals
p, q , r
reflections in edges:
rotations at corners:
a , b, c



,
,
angles at corners:
l m n
terminology: (l,m,n) -triangle, (s,t,u,v) quadrilateral, etc.,
9
Tiling: The Master Tile - 3


terminology: (l,m,n) -triangle, (s,t,u,v) quadrilateral, etc.
hyperbolic when   2 or
 2

l


m


n

or
1
1
1
1 

0
l
m
n
10
The Tiling Group
Observe/define:
a  pq , b  qr , c  rp
Tiling Group:
G   p, q , r 
*
Orientation Preserving Tiling Group:
G   a , b, c 
11
Group Relations (simple geometric
and group theoretic proofs)
p q r
2
a b
n
2
l
2
m
 1.
 c  1,
abc  1, ( pqqrrp  1)
 ( a )  qaq  qpqq  qp  a ,
1
1
 (b)  qbq  qqrq  rq  b .
1
1
12
Riemann Hurwitz equation
( euler characteristic proof)
Let S be a surface of genus

then:
2  2
1 1 1
 1  
| G|
l m n
13
Tiling Theorem
A surface S of genus
tiling group

has a tiling with
G   p, q , r 
*
if and only if
 the group relations hold
 the Riemann Hurwitz equation holds
14
Tiling Problems - Student Projects




Tilings of low genus (Ryan Vinroot)
Divisible tilings (Dawn Haney, Lori
McKeough)
Splitting reflections (Jim Belk)
Tilings and Cwatsets (Reva Schweitzer and
Patrick Swickard)
15
Divisible Tilings




torus - euclidean plane example
hyperbolic plane example
Dawn & Lori’s results
group theoretic surprise
16
Torus example ((2,2,2,2) by (2,4,4))
17
Euclidean Plane Example
((2,2,2,2) by (2,4,4))


show picture
the Euclidean plane is the “unwrapping” of
torus “universal cover”
18
Hyperbolic Plane Example


show picture
can’t draw tiled surfaces so we work in
hyperbolic plane, the universal cover
19
Dawn and Lori’s Problem and Results




Problem find divisible quadrilaterals
restricted search to quadrilaterals with one
triangle in each corner
show picture
used Maple to do
– combinatorial search
– group theoretic computations in 2x2 complex
matrices
20
Dawn & Lori’s Problem and Results
cont’d

Conjecture: Every divisible tiling (with a
single tile in the corner is symmetric
21
A group theoretic surprise



we have found divisible tilings in
hyperbolic plane
Now find surface of smallest genus with the
same divisible tiling
for (2,3,7) tiling of (3,7,3,7) we have:
| G |  2357200374260265501327360000
*
  14030954608692056555520001
22
A group theoretic surprise - cont’d
| G |  2  22! and
*
21
1  Z  G   22  1
21
2
*
23
Thank You!
Questions???
24