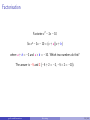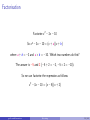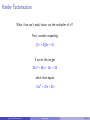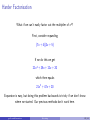* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Factorising - Numeracy Workshop
Quartic function wikipedia , lookup
Horner's method wikipedia , lookup
Gröbner basis wikipedia , lookup
Cayley–Hamilton theorem wikipedia , lookup
System of polynomial equations wikipedia , lookup
Polynomial ring wikipedia , lookup
Polynomial greatest common divisor wikipedia , lookup
Fundamental theorem of algebra wikipedia , lookup
Factorization of polynomials over finite fields wikipedia , lookup
Please Note These pdf slides are configured for viewing on a computer screen. Viewing them on hand-held devices may be difficult as they require a “slideshow” mode. Do not try to print them out as there are many more pages than the number of slides listed at the bottom right of each screen. Apologies for any inconvenience. Factorising Numeracy Workshop geoff.coates@uwa.edu.au geoff.coates@uwa.edu.au Factorising 2 / 43 Introduction These slides extend on a basic knowledge of algebra (such as the previous Algebra workshop Expressions and Expansion). Topics include extracting common factors, factorising quadratic expressions and polynomials. geoff.coates@uwa.edu.au Factorising 3 / 43 Introduction These slides extend on a basic knowledge of algebra (such as the previous Algebra workshop Expressions and Expansion). Topics include extracting common factors, factorising quadratic expressions and polynomials. Workshop resources: These slides are available online: www.studysmarter.uwa.edu.au → Numeracy and Maths → Online Resources geoff.coates@uwa.edu.au Factorising 3 / 43 Introduction These slides extend on a basic knowledge of algebra (such as the previous Algebra workshop Expressions and Expansion). Topics include extracting common factors, factorising quadratic expressions and polynomials. Workshop resources: These slides are available online: www.studysmarter.uwa.edu.au → Numeracy and Maths → Online Resources Next Workshop: See your Workshop Calendar → www.studysmarter.uwa.edu.au geoff.coates@uwa.edu.au Factorising 3 / 43 Introduction These slides extend on a basic knowledge of algebra (such as the previous Algebra workshop Expressions and Expansion). Topics include extracting common factors, factorising quadratic expressions and polynomials. Workshop resources: These slides are available online: www.studysmarter.uwa.edu.au → Numeracy and Maths → Online Resources Next Workshop: See your Workshop Calendar → www.studysmarter.uwa.edu.au Drop-in Study Sessions: Monday, Wednesday, Friday, 10am-12pm, Room 2202, Second Floor, Social Sciences South Building, every week. geoff.coates@uwa.edu.au Factorising 3 / 43 Introduction These slides extend on a basic knowledge of algebra (such as the previous Algebra workshop Expressions and Expansion). Topics include extracting common factors, factorising quadratic expressions and polynomials. Workshop resources: These slides are available online: www.studysmarter.uwa.edu.au → Numeracy and Maths → Online Resources Next Workshop: See your Workshop Calendar → www.studysmarter.uwa.edu.au Drop-in Study Sessions: Monday, Wednesday, Friday, 10am-12pm, Room 2202, Second Floor, Social Sciences South Building, every week. Email: geoff.coates@uwa.edu.au geoff.coates@uwa.edu.au Factorising 3 / 43 Factors of numbers A factor of a number is a number that divides into it evenly. geoff.coates@uwa.edu.au Factorising 4 / 43 Factors of numbers A factor of a number is a number that divides into it evenly. Example: 4 is a factor of 12 since 3 × 4 = 12. geoff.coates@uwa.edu.au Factorising 4 / 43 Factors of numbers A factor of a number is a number that divides into it evenly. Example: 4 is a factor of 12 since 3 × 4 = 12. Of course, 3 is also a factor of 12. geoff.coates@uwa.edu.au Factorising 4 / 43 Factors of numbers A factor of a number is a number that divides into it evenly. Example: 4 is a factor of 12 since 3 × 4 = 12. Of course, 3 is also a factor of 12. (The others are geoff.coates@uwa.edu.au Factorising 4 / 43 Factors of numbers A factor of a number is a number that divides into it evenly. Example: 4 is a factor of 12 since 3 × 4 = 12. Of course, 3 is also a factor of 12. (The others are 1, 2, 6 and 12.) geoff.coates@uwa.edu.au Factorising 4 / 43 Factors of terms A factor of a term is a number, variable or combination that divides into it evenly. geoff.coates@uwa.edu.au Factorising 5 / 43 Factors of terms A factor of a term is a number, variable or combination that divides into it evenly. Example: The term 12x has a factor of 4 since 3x × 4 = 12x. geoff.coates@uwa.edu.au Factorising 5 / 43 Factors of terms A factor of a term is a number, variable or combination that divides into it evenly. Example: The term 12x has a factor of 4 since 3x × 4 = 12x. Important point: the variable x is also a factor of 12x since 12 × x = 12x. (This is true even though x could be any number, including non-whole numbers.) geoff.coates@uwa.edu.au Factorising 5 / 43 Factors of terms A factor of a term is a number, variable or combination that divides into it evenly. Example: The term 12x has a factor of 4 since 3x × 4 = 12x. Important point: the variable x is also a factor of 12x since 12 × x = 12x. (This is true even though x could be any number, including non-whole numbers.) Factors of 12x can be made up of combinations of other factors, such as geoff.coates@uwa.edu.au Factorising 5 / 43 Factors of terms A factor of a term is a number, variable or combination that divides into it evenly. Example: The term 12x has a factor of 4 since 3x × 4 = 12x. Important point: the variable x is also a factor of 12x since 12 × x = 12x. (This is true even though x could be any number, including non-whole numbers.) Factors of 12x can be made up of combinations of other factors, such as 2, 6x, 1, 3x, 12, etc. geoff.coates@uwa.edu.au Factorising 5 / 43 Factors of expressions In the previous algebra workshop we looked at the expression 4(2x + 3) geoff.coates@uwa.edu.au Factorising 6 / 43 Factors of expressions In the previous algebra workshop we looked at the expression 4(2x + 3) This has two clear factors, geoff.coates@uwa.edu.au Factorising 6 / 43 Factors of expressions In the previous algebra workshop we looked at the expression 4(2x + 3) This has two clear factors, 4 and geoff.coates@uwa.edu.au Factorising 6 / 43 Factors of expressions In the previous algebra workshop we looked at the expression 4(2x + 3) This has two clear factors, 4 and 2x + 3 because 4 × (2x + 3) = 4(2x + 3) geoff.coates@uwa.edu.au Factorising 6 / 43 Factors of expressions In the previous algebra workshop we looked at the expression 4(2x + 3) This has two clear factors, 4 and 2x + 3 because 4 × (2x + 3) = 4(2x + 3) When we expanded the brackets, we got 4(2x + 3) = 8x + 12 geoff.coates@uwa.edu.au Factorising 6 / 43 Factors of expressions In the previous algebra workshop we looked at the expression 4(2x + 3) This has two clear factors, 4 and 2x + 3 because 4 × (2x + 3) = 4(2x + 3) When we expanded the brackets, we got 4(2x + 3) = 8x + 12 Our task now is to reverse this process. geoff.coates@uwa.edu.au Factorising 6 / 43 Factors of expressions In the previous algebra workshop we looked at the expression 4(2x + 3) This has two clear factors, 4 and 2x + 3 because 4 × (2x + 3) = 4(2x + 3) When we expanded the brackets, we got 4(2x + 3) = 8x + 12 Our task now is to reverse this process. That is, take an expression like 8x + 12 and extract the factors which are common to both terms (8x and 12). geoff.coates@uwa.edu.au Factorising 6 / 43 Factors of expressions In the previous algebra workshop we looked at the expression 4(2x + 3) This has two clear factors, 4 and 2x + 3 because 4 × (2x + 3) = 4(2x + 3) When we expanded the brackets, we got 4(2x + 3) = 8x + 12 Our task now is to reverse this process. That is, take an expression like 8x + 12 and extract the factors which are common to both terms (8x and 12). This process is called factorisation. geoff.coates@uwa.edu.au Factorising 6 / 43 Factorisation example Example: Factorise 28x + 98x 2 . geoff.coates@uwa.edu.au Factorising 7 / 43 Factorisation example Example: Factorise 28x + 98x 2 . What factors do the terms 28x and 98x 2 have in common? geoff.coates@uwa.edu.au Factorising 7 / 43 Factorisation example Example: Factorise 28x + 98x 2 . What factors do the terms 28x and 98x 2 have in common? It might help to imagine some multiplication signs: 28 × x geoff.coates@uwa.edu.au and Factorising 98 × x × x 7 / 43 Factorisation example Example: Factorise 28x + 98x 2 . What factors do the terms 28x and 98x 2 have in common? It might help to imagine some multiplication signs: 28 × x and 98 × x × x So, x is a factor common to both terms. geoff.coates@uwa.edu.au Factorising 7 / 43 Factorisation example Example: Factorise 28x + 98x 2 . What factors do the terms 28x and 98x 2 have in common? It might help to imagine some multiplication signs: 28 × x and 98 × x × x So, x is a factor common to both terms. Both numbers are even: geoff.coates@uwa.edu.au Factorising 7 / 43 Factorisation example Example: Factorise 28x + 98x 2 . What factors do the terms 28x and 98x 2 have in common? It might help to imagine some multiplication signs: 28 × x and 98 × x × x So, x is a factor common to both terms. Both numbers are even: 2 × 14 × x geoff.coates@uwa.edu.au and Factorising 2 × 49 × x × x 7 / 43 Factorisation example Example: Factorise 28x + 98x 2 . What factors do the terms 28x and 98x 2 have in common? It might help to imagine some multiplication signs: 28 × x and 98 × x × x So, x is a factor common to both terms. Both numbers are even: 2 × 14 × x and 2 × 49 × x × x So, 2 is also a common factor. geoff.coates@uwa.edu.au Factorising 7 / 43 Factorisation example Example: Factorise 28x + 98x 2 . What factors do the terms 28x and 98x 2 have in common? It might help to imagine some multiplication signs: 28 × x and 98 × x × x So, x is a factor common to both terms. Both numbers are even: 2 × 14 × x and 2 × 49 × x × x So, 2 is also a common factor. In fact, this step reveals another one. geoff.coates@uwa.edu.au Factorising 7 / 43 Factorisation example Example: Factorise 28x + 98x 2 . What factors do the terms 28x and 98x 2 have in common? It might help to imagine some multiplication signs: 28 × x and 98 × x × x So, x is a factor common to both terms. Both numbers are even: 2 × 14 × x and 2 × 49 × x × x So, 2 is also a common factor. In fact, this step reveals another one. 2×2×7×x geoff.coates@uwa.edu.au and Factorising 2×7×7×x ×x 7 / 43 Factorisation example Example: Factorise 28x + 98x 2 . What factors do the terms 28x and 98x 2 have in common? It might help to imagine some multiplication signs: 28 × x and 98 × x × x So, x is a factor common to both terms. Both numbers are even: 2 × 14 × x and 2 × 49 × x × x So, 2 is also a common factor. In fact, this step reveals another one. 2×2×7×x and 2×7×7×x ×x 7 is also a common factor. geoff.coates@uwa.edu.au Factorising 7 / 43 Factorisation example Example: Factorise 28x + 98x 2 . 2×2×7×x geoff.coates@uwa.edu.au and Factorising 2×7×7×x ×x 8 / 43 Factorisation example Example: Factorise 28x + 98x 2 . 2×2×7×x and 2×7×7×x ×x The combination of common factors is 2 × 7 × x = 14x. geoff.coates@uwa.edu.au Factorising 8 / 43 Factorisation example Example: Factorise 28x + 98x 2 . 2×2×7×x and 2×7×7×x ×x The combination of common factors is 2 × 7 × x = 14x. We call this the highest common factor and write it outside some brackets: geoff.coates@uwa.edu.au Factorising 8 / 43 Factorisation example Example: Factorise 28x + 98x 2 . 2×2×7×x and 2×7×7×x ×x The combination of common factors is 2 × 7 × x = 14x. We call this the highest common factor and write it outside some brackets: 28x + 98x 2 = 14x( geoff.coates@uwa.edu.au Factorising ) 8 / 43 Factorisation example Example: Factorise 28x + 98x 2 . 2×2×7×x and 2×7×7×x ×x The combination of common factors is 2 × 7 × x = 14x. We call this the highest common factor and write it outside some brackets: 28x + 98x 2 = 14x( ) The remaining bits of both terms go inside the brackets. geoff.coates@uwa.edu.au Factorising 8 / 43 Factorisation example Example: Factorise 28x + 98x 2 . 2×2×7×x and 2×7×7×x ×x The combination of common factors is 2 × 7 × x = 14x. We call this the highest common factor and write it outside some brackets: 28x + 98x 2 = 14x(2 + 7x) The remaining bits of both terms go inside the brackets. geoff.coates@uwa.edu.au Factorising 8 / 43 Factorisation example Example: Factorise 28x + 98x 2 . 2×2×7×x and 2×7×7×x ×x The combination of common factors is 2 × 7 × x = 14x. We call this the highest common factor and write it outside some brackets: 28x + 98x 2 = 14x(2 + 7x) The remaining bits of both terms go inside the brackets. This is the fully factorised form of the original expression. geoff.coates@uwa.edu.au Factorising 8 / 43 Factorisation example Example: Factorise 28x + 98x 2 . 2×2×7×x and 2×7×7×x ×x The combination of common factors is 2 × 7 × x = 14x. We call this the highest common factor and write it outside some brackets: 28x + 98x 2 = 14x(2 + 7x) The remaining bits of both terms go inside the brackets. This is the fully factorised form of the original expression. Note: You can check your answer by expanding the factorised form. geoff.coates@uwa.edu.au Factorising 8 / 43 Factorisation exercises 6x − 3x 2 = geoff.coates@uwa.edu.au Factorising 9 / 43 Factorisation exercises 6x − 3x 2 = 3x( geoff.coates@uwa.edu.au Factorising ) 9 / 43 Factorisation exercises 6x − 3x 2 = 3x(2 − x) geoff.coates@uwa.edu.au Factorising 9 / 43 Factorisation exercises 6x − 3x 2 = 3x(2 − x) 8y + 16y 2 = geoff.coates@uwa.edu.au Factorising 9 / 43 Factorisation exercises 6x − 3x 2 = 3x(2 − x) 8y + 16y 2 = 8y ( geoff.coates@uwa.edu.au Factorising ) 9 / 43 Factorisation exercises 6x − 3x 2 = 3x(2 − x) 8y + 16y 2 = 8y (1 + 2y ) geoff.coates@uwa.edu.au Factorising 9 / 43 Factorisation exercises 6x − 3x 2 = 3x(2 − x) 8y + 16y 2 = 8y (1 + 2y ) (Note the use of the “hidden” factor of 1 in the first term.) geoff.coates@uwa.edu.au Factorising 9 / 43 Factorisation exercises 6x − 3x 2 = 3x(2 − x) 8y + 16y 2 = 8y (1 + 2y ) (Note the use of the “hidden” factor of 1 in the first term.) 2x 2 y + 4x 3 = geoff.coates@uwa.edu.au Factorising 9 / 43 Factorisation exercises 6x − 3x 2 = 3x(2 − x) 8y + 16y 2 = 8y (1 + 2y ) (Note the use of the “hidden” factor of 1 in the first term.) 2x 2 y + 4x 3 = 2x 2 ( geoff.coates@uwa.edu.au Factorising ) 9 / 43 Factorisation exercises 6x − 3x 2 = 3x(2 − x) 8y + 16y 2 = 8y (1 + 2y ) (Note the use of the “hidden” factor of 1 in the first term.) 2x 2 y + 4x 3 = 2x 2 (y + 2x) geoff.coates@uwa.edu.au Factorising 9 / 43 Factorisation exercises 6x − 3x 2 = 3x(2 − x) 8y + 16y 2 = 8y (1 + 2y ) (Note the use of the “hidden” factor of 1 in the first term.) 2x 2 y + 4x 3 = 2x 2 (y + 2x) 2xy − 4x + 3x 2 = geoff.coates@uwa.edu.au Factorising 9 / 43 Factorisation exercises 6x − 3x 2 = 3x(2 − x) 8y + 16y 2 = 8y (1 + 2y ) (Note the use of the “hidden” factor of 1 in the first term.) 2x 2 y + 4x 3 = 2x 2 (y + 2x) 2xy − 4x + 3x 2 = x( geoff.coates@uwa.edu.au Factorising ) 9 / 43 Factorisation exercises 6x − 3x 2 = 3x(2 − x) 8y + 16y 2 = 8y (1 + 2y ) (Note the use of the “hidden” factor of 1 in the first term.) 2x 2 y + 4x 3 = 2x 2 (y + 2x) 2xy − 4x + 3x 2 = x(2y − 4 + 3x) geoff.coates@uwa.edu.au Factorising 9 / 43 Factorisation exercises 6x − 3x 2 = 3x(2 − x) 8y + 16y 2 = 8y (1 + 2y ) (Note the use of the “hidden” factor of 1 in the first term.) 2x 2 y + 4x 3 = 2x 2 (y + 2x) 2xy − 4x + 3x 2 = x(2y − 4 + 3x) (Factors must be common to all terms.) geoff.coates@uwa.edu.au Factorising 9 / 43 Double bracket expressions Here is a common type of double bracket expression. (x + 2)(x + 5) = geoff.coates@uwa.edu.au Factorising 10 / 43 Double bracket expressions Here is a common type of double bracket expression. Let’s expand the brackets to see whether there are any useful patterns we can use to reverse the process: (x + 2)(x + 5) = geoff.coates@uwa.edu.au Factorising 10 / 43 Double bracket expressions Here is a common type of double bracket expression. Let’s expand the brackets to see whether there are any useful patterns we can use to reverse the process: (x + 2)(x + 5) = geoff.coates@uwa.edu.au Factorising 10 / 43 Double bracket expressions Here is a common type of double bracket expression. Let’s expand the brackets to see whether there are any useful patterns we can use to reverse the process: (x + 2)(x + 5) = x 2 geoff.coates@uwa.edu.au Factorising 10 / 43 Double bracket expressions Here is a common type of double bracket expression. Let’s expand the brackets to see whether there are any useful patterns we can use to reverse the process: (x + 2)(x + 5) = x 2 geoff.coates@uwa.edu.au Factorising 10 / 43 Double bracket expressions Here is a common type of double bracket expression. Let’s expand the brackets to see whether there are any useful patterns we can use to reverse the process: (x + 2)(x + 5) = x 2 + 5x geoff.coates@uwa.edu.au Factorising 10 / 43 Double bracket expressions Here is a common type of double bracket expression. Let’s expand the brackets to see whether there are any useful patterns we can use to reverse the process: (x + 2)(x + 5) = x 2 + 5x geoff.coates@uwa.edu.au Factorising 10 / 43 Double bracket expressions Here is a common type of double bracket expression. Let’s expand the brackets to see whether there are any useful patterns we can use to reverse the process: (x + 2)(x + 5) = x 2 + 5x + 2x geoff.coates@uwa.edu.au Factorising 10 / 43 Double bracket expressions Here is a common type of double bracket expression. Let’s expand the brackets to see whether there are any useful patterns we can use to reverse the process: (x + 2)(x + 5) = x 2 + 5x + 2x geoff.coates@uwa.edu.au Factorising 10 / 43 Double bracket expressions Here is a common type of double bracket expression. Let’s expand the brackets to see whether there are any useful patterns we can use to reverse the process: (x + 2)(x + 5) = x 2 + 5x + 2x + 2 × 5 geoff.coates@uwa.edu.au Factorising 10 / 43 Double bracket expressions Here is a common type of double bracket expression. Let’s expand the brackets to see whether there are any useful patterns we can use to reverse the process: (x + 2)(x + 5) = x 2 + 5x + 2x + 2 × 5 = x 2 + (5 + 2)x + 2 × 5 geoff.coates@uwa.edu.au Factorising 10 / 43 Double bracket expressions Here is a common type of double bracket expression. Let’s expand the brackets to see whether there are any useful patterns we can use to reverse the process: (x + 2)(x + 5) = x 2 + 5x + 2x + 2 × 5 = x 2 + (5 + 2)x + 2 × 5 = x2 + geoff.coates@uwa.edu.au Factorising 7x + 10 10 / 43 Double bracket expressions Here is a common type of double bracket expression. Let’s expand the brackets to see whether there are any useful patterns we can use to reverse the process: (x + 2)(x + 5) = x 2 + 5x + 2x + 2 × 5 = x 2 + (5 + 2)x + 2 × 5 = x2 + 7x + 10 The pattern is here: 5 + 2 = 7 and 2 × 5 = 10. geoff.coates@uwa.edu.au Factorising 10 / 43 A Rule So, in general, whenever we are asked to expand an expression of the form: (x + a)(x + b) geoff.coates@uwa.edu.au Factorising 11 / 43 A Rule So, in general, whenever we are asked to expand an expression of the form: (x + a)(x + b) we always end up with x 2 + (a + b)x + ab That is, you always add the two numbers a and b together to get the number multiplying x, and you multiply them to get the constant term. geoff.coates@uwa.edu.au Factorising 11 / 43 Factorisation If we are asked to factorise: x 2 + 5x + 6 then we are being asked to write the above in the form (x + a)(x + b) geoff.coates@uwa.edu.au Factorising 12 / 43 Factorisation If we are asked to factorise: x 2 + 5x + 6 then we are being asked to write the above in the form (x + a)(x + b) where a + b = 5 and a × b = 6. Can you find two numbers which do this? geoff.coates@uwa.edu.au Factorising 12 / 43 Factorisation If we are asked to factorise: x 2 + 5x + 6 then we are being asked to write the above in the form (x + a)(x + b) where a + b = 5 and a × b = 6. Can you find two numbers which do this? The answer is 2 and 3 (2 + 3 = 5, 2 × 3 = 6). geoff.coates@uwa.edu.au Factorising 12 / 43 Factorisation If we are asked to factorise: x 2 + 5x + 6 then we are being asked to write the above in the form (x + a)(x + b) where a + b = 5 and a × b = 6. Can you find two numbers which do this? The answer is 2 and 3 (2 + 3 = 5, 2 × 3 = 6). So we can factorise the expression as follows: x 2 + 5x + 6 = (x + 2)(x + 3) geoff.coates@uwa.edu.au Factorising 12 / 43 Factorisation Factorise x 2 − 3x − 10 geoff.coates@uwa.edu.au Factorising 13 / 43 Factorisation Factorise x 2 − 3x − 10 So x 2 − 3x − 10 = (x + a)(x + b) where a + b = −3 and a × b = −10. Which two numbers do this? geoff.coates@uwa.edu.au Factorising 13 / 43 Factorisation Factorise x 2 − 3x − 10 So x 2 − 3x − 10 = (x + a)(x + b) where a + b = −3 and a × b = −10. Which two numbers do this? The answer is −5 and 2 (−5 + 2 = −3, −5 × 2 = −10). geoff.coates@uwa.edu.au Factorising 13 / 43 Factorisation Factorise x 2 − 3x − 10 So x 2 − 3x − 10 = (x + a)(x + b) where a + b = −3 and a × b = −10. Which two numbers do this? The answer is −5 and 2 (−5 + 2 = −3, −5 × 2 = −10). So we can factorise the expression as follows: x 2 − 3x − 10 = (x − 5)(x + 2) geoff.coates@uwa.edu.au Factorising 13 / 43 Removing Factors We have seen a method which usually works when the multiplier of x 2 is equal to 1. What if we were asked to factorise: 3x 2 + 9x + 6 geoff.coates@uwa.edu.au Factorising 14 / 43 Removing Factors We have seen a method which usually works when the multiplier of x 2 is equal to 1. What if we were asked to factorise: 3x 2 + 9x + 6 We notice that the multipliers of all three terms in the above expression are divisible by 3. Hence, we can factor out this common factor as follows: 3x 2 + 9x + 6 = 3(x 2 + 3x + 2) geoff.coates@uwa.edu.au Factorising 14 / 43 Removing Factors We have seen a method which usually works when the multiplier of x 2 is equal to 1. What if we were asked to factorise: 3x 2 + 9x + 6 We notice that the multipliers of all three terms in the above expression are divisible by 3. Hence, we can factor out this common factor as follows: 3x 2 + 9x + 6 = 3(x 2 + 3x + 2) Now, the expression in brackets is just like we saw on the previous slides, we look for two numbers which add to 3 and multiply to 2. This gives us: 3x 2 + 9x + 6 = 3 geoff.coates@uwa.edu.au Factorising 14 / 43 Removing Factors We have seen a method which usually works when the multiplier of x 2 is equal to 1. What if we were asked to factorise: 3x 2 + 9x + 6 We notice that the multipliers of all three terms in the above expression are divisible by 3. Hence, we can factor out this common factor as follows: 3x 2 + 9x + 6 = 3(x 2 + 3x + 2) Now, the expression in brackets is just like we saw on the previous slides, we look for two numbers which add to 3 and multiply to 2. This gives us: 3x 2 + 9x + 6 = 3(x + 1)(x + 2) geoff.coates@uwa.edu.au Factorising 14 / 43 Removing Factors Factorise the following expression. 5x 2 + 40x + 60 geoff.coates@uwa.edu.au Factorising 15 / 43 Removing Factors Factorise the following expression. 5x 2 + 40x + 60 Here we see that the multiplier of x 2 is 5. We also notice that all multipliers in the above expression are divisible by 5. Hence, we can factor out this common factor as follows: 5x 2 + 40x + 60 = 5(x 2 + 8x + 12) geoff.coates@uwa.edu.au Factorising 15 / 43 Removing Factors Factorise the following expression. 5x 2 + 40x + 60 Here we see that the multiplier of x 2 is 5. We also notice that all multipliers in the above expression are divisible by 5. Hence, we can factor out this common factor as follows: 5x 2 + 40x + 60 = 5(x 2 + 8x + 12) Now we look for two numbers which add to 8 and multiply to 12. This gives us: 5x 2 + 40x + 60 = 5 geoff.coates@uwa.edu.au Factorising 15 / 43 Removing Factors Factorise the following expression. 5x 2 + 40x + 60 Here we see that the multiplier of x 2 is 5. We also notice that all multipliers in the above expression are divisible by 5. Hence, we can factor out this common factor as follows: 5x 2 + 40x + 60 = 5(x 2 + 8x + 12) Now we look for two numbers which add to 8 and multiply to 12. This gives us: 5x 2 + 40x + 60 = 5(x + 2)(x + 6) geoff.coates@uwa.edu.au Factorising 15 / 43 Factorisation If we are asked to factorise: x2 − 9 then we are being asked to write the above in the form (x + a)(x + b) geoff.coates@uwa.edu.au Factorising 16 / 43 Factorisation If we are asked to factorise: x2 − 9 then we are being asked to write the above in the form (x + a)(x + b) It looks different to the expressions we have been factorising because it appears to have no x term. geoff.coates@uwa.edu.au Factorising 16 / 43 Factorisation If we are asked to factorise: x2 − 9 then we are being asked to write the above in the form (x + a)(x + b) It looks different to the expressions we have been factorising because it appears to have no x term. However, we can make it the same if we include an x term with a multiplier of geoff.coates@uwa.edu.au Factorising 16 / 43 Factorisation If we are asked to factorise: x2 − 9 then we are being asked to write the above in the form (x + a)(x + b) It looks different to the expressions we have been factorising because it appears to have no x term. However, we can make it the same if we include an x term with a multiplier of 0: x 2 +0x − 9 geoff.coates@uwa.edu.au Factorising 16 / 43 Factorisation If we are asked to factorise: x2 − 9 then we are being asked to write the above in the form (x + a)(x + b) It looks different to the expressions we have been factorising because it appears to have no x term. However, we can make it the same if we include an x term with a multiplier of 0: x 2 +0x − 9 So we know that we need two numbers which add up to 0 and multiply to give −9. Can you find two numbers which do this? geoff.coates@uwa.edu.au Factorising 16 / 43 Factorisation If we are asked to factorise: x2 − 9 then we are being asked to write the above in the form (x + a)(x + b) It looks different to the expressions we have been factorising because it appears to have no x term. However, we can make it the same if we include an x term with a multiplier of 0: x 2 +0x − 9 So we know that we need two numbers which add up to 0 and multiply to give −9. Can you find two numbers which do this? The answer is 3 and −3 (3 + −3 = 0, 3 × −3 = −9). geoff.coates@uwa.edu.au Factorising 16 / 43 Factorisation If we are asked to factorise: x2 − 9 then we are being asked to write the above in the form (x + a)(x + b) It looks different to the expressions we have been factorising because it appears to have no x term. However, we can make it the same if we include an x term with a multiplier of 0: x 2 +0x − 9 So we know that we need two numbers which add up to 0 and multiply to give −9. Can you find two numbers which do this? The answer is 3 and −3 (3 + −3 = 0, 3 × −3 = −9). So we can factorise the expression as follows: x 2 − 9 = (x + 3)(x − 3) geoff.coates@uwa.edu.au Factorising 16 / 43 The Difference of Two Squares If you are asked to factorise x 2 − 16 we get: geoff.coates@uwa.edu.au Factorising 17 / 43 The Difference of Two Squares If you are asked to factorise x 2 − 16 we get: (x + 4)(x − 4) geoff.coates@uwa.edu.au Factorising 17 / 43 The Difference of Two Squares If you are asked to factorise x 2 − 16 we get: (x + 4)(x − 4) If you are asked to factorise x 2 − 36 we get: geoff.coates@uwa.edu.au Factorising 17 / 43 The Difference of Two Squares If you are asked to factorise x 2 − 16 we get: (x + 4)(x − 4) If you are asked to factorise x 2 − 36 we get: (x + 6)(x − 6) geoff.coates@uwa.edu.au Factorising 17 / 43 The Difference of Two Squares If you are asked to factorise x 2 − 16 we get: (x + 4)(x − 4) If you are asked to factorise x 2 − 36 we get: (x + 6)(x − 6) This leads us to a general formula called the difference of two squares: x 2 − a2 = (x + a)(x − a) geoff.coates@uwa.edu.au Factorising 17 / 43 The Difference of Two Squares If you are asked to factorise x 2 − 16 we get: (x + 4)(x − 4) If you are asked to factorise x 2 − 36 we get: (x + 6)(x − 6) This leads us to a general formula called the difference of two squares: x 2 − a2 = (x + a)(x − a) Tip: Try to avoid memorising too many formulas. It’s handy to remember that this is just a simple special case of a more general process. geoff.coates@uwa.edu.au Factorising 17 / 43 The Difference of Two Squares: Examples x 2 − 25 geoff.coates@uwa.edu.au = Factorising 18 / 43 The Difference of Two Squares: Examples x 2 − 25 geoff.coates@uwa.edu.au = (x − 5)(x + 5) Factorising 18 / 43 The Difference of Two Squares: Examples geoff.coates@uwa.edu.au x 2 − 25 = (x − 5)(x + 5) x 2 − 49 = Factorising 18 / 43 The Difference of Two Squares: Examples geoff.coates@uwa.edu.au x 2 − 25 = (x − 5)(x + 5) x 2 − 49 = (x + 7)(x − 7) Factorising 18 / 43 The Difference of Two Squares: Examples x 2 − 25 = (x − 5)(x + 5) x 2 − 49 = (x + 7)(x − 7) 4x 2 − 25 geoff.coates@uwa.edu.au = Factorising 18 / 43 The Difference of Two Squares: Examples x 2 − 25 = (x − 5)(x + 5) x 2 − 49 = (x + 7)(x − 7) 4x 2 − 25 = (2x)2 − 52 = geoff.coates@uwa.edu.au Factorising 18 / 43 The Difference of Two Squares: Examples x 2 − 25 = (x − 5)(x + 5) x 2 − 49 = (x + 7)(x − 7) 4x 2 − 25 geoff.coates@uwa.edu.au = (2x)2 − 52 = (2x − 5)(2x + 5) Factorising 18 / 43 The Difference of Two Squares: Examples x 2 − 25 = (x − 5)(x + 5) x 2 − 49 = (x + 7)(x − 7) 4x 2 − 25 9x 4 − 64 geoff.coates@uwa.edu.au = (2x)2 − 52 = (2x − 5)(2x + 5) = Factorising 18 / 43 The Difference of Two Squares: Examples x 2 − 25 = (x − 5)(x + 5) x 2 − 49 = (x + 7)(x − 7) 4x 2 − 25 9x 4 − 64 = (2x)2 − 52 = (2x − 5)(2x + 5) = 3x 2 2 − 82 = geoff.coates@uwa.edu.au Factorising 18 / 43 The Difference of Two Squares: Examples x 2 − 25 = (x − 5)(x + 5) x 2 − 49 = (x + 7)(x − 7) 4x 2 − 25 9x 4 − 64 = (2x)2 − 52 = (2x − 5)(2x + 5) = = geoff.coates@uwa.edu.au 3x 2 2 − 82 3x 2 − 8 3x 2 + 8 Factorising 18 / 43 The Difference of Two Squares: Examples Sometimes we need to factor out the highest common factor: 3x 2 − 75 geoff.coates@uwa.edu.au = Factorising 19 / 43 The Difference of Two Squares: Examples Sometimes we need to factor out the highest common factor: 3x 2 − 75 = 3(x 2 − 25) = geoff.coates@uwa.edu.au 3 Factorising 19 / 43 The Difference of Two Squares: Examples Sometimes we need to factor out the highest common factor: 3x 2 − 75 = 3(x 2 − 25) = geoff.coates@uwa.edu.au 3(x + 5)(x − 5) Factorising 19 / 43 The Difference of Two Squares: Examples Sometimes we need to factor out the highest common factor: 3x 2 − 75 = 3(x 2 − 25) = 2x 2 − 8 geoff.coates@uwa.edu.au 3(x + 5)(x − 5) = Factorising 19 / 43 The Difference of Two Squares: Examples Sometimes we need to factor out the highest common factor: 3x 2 − 75 2x 2 − 8 geoff.coates@uwa.edu.au = 3(x 2 − 25) = 3(x + 5)(x − 5) = = 2(x 2 − 4) 2 Factorising 19 / 43 The Difference of Two Squares: Examples Sometimes we need to factor out the highest common factor: 3x 2 − 75 2x 2 − 8 geoff.coates@uwa.edu.au = 3(x 2 − 25) = 3(x + 5)(x − 5) = = 2(x 2 − 4) 2(x + 2)(x − 2) Factorising 19 / 43 The Difference of Two Squares: Examples Sometimes we need to factor out the highest common factor: 3x 2 − 75 geoff.coates@uwa.edu.au = 3(x 2 − 25) = 3(x + 5)(x − 5) 2x 2 − 8 = = 2(x 2 − 4) 2(x + 2)(x − 2) x 3 − 25x = Factorising 19 / 43 The Difference of Two Squares: Examples Sometimes we need to factor out the highest common factor: 3x 2 − 75 2x 2 − 8 x 3 − 25x = 3(x 2 − 25) = 3(x + 5)(x − 5) = = 2(x 2 − 4) 2(x + 2)(x − 2) = x(x 2 − 25) = x geoff.coates@uwa.edu.au Factorising 19 / 43 The Difference of Two Squares: Examples Sometimes we need to factor out the highest common factor: 3x 2 − 75 2x 2 − 8 x 3 − 25x = 3(x 2 − 25) = 3(x + 5)(x − 5) = = 2(x 2 − 4) 2(x + 2)(x − 2) = x(x 2 − 25) = x(x − 5)(x + 5) geoff.coates@uwa.edu.au Factorising 19 / 43 The Difference of Two Squares: Examples Sometimes we need to factor out the highest common factor: 3x 2 − 75 2x 2 − 8 x 3 − 25x = 3(x 2 − 25) = 3(x + 5)(x − 5) = = 2(x 2 − 4) 2(x + 2)(x − 2) = x(x 2 − 25) = x(x − 5)(x + 5) 18x 3 − 32x geoff.coates@uwa.edu.au = Factorising 19 / 43 The Difference of Two Squares: Examples Sometimes we need to factor out the highest common factor: 3x 2 − 75 2x 2 − 8 x 3 − 25x = 3(x 2 − 25) = 3(x + 5)(x − 5) = = 2(x 2 − 4) 2(x + 2)(x − 2) = x(x 2 − 25) = x(x − 5)(x + 5) 18x 3 − 32x geoff.coates@uwa.edu.au = = 2x(9x 2 − 16) 2x Factorising 19 / 43 The Difference of Two Squares: Examples Sometimes we need to factor out the highest common factor: 3x 2 − 75 2x 2 − 8 x 3 − 25x = 3(x 2 − 25) = 3(x + 5)(x − 5) = = 2(x 2 − 4) 2(x + 2)(x − 2) = x(x 2 − 25) = x(x − 5)(x + 5) 18x 3 − 32x geoff.coates@uwa.edu.au = = 2x(9x 2 − 16) 2x(3x + 4)(3x − 4) Factorising 19 / 43 Harder Factorisation What if we can’t easily factor out the multiplier of x 2 ? geoff.coates@uwa.edu.au Factorising 20 / 43 Harder Factorisation What if we can’t easily factor out the multiplier of x 2 ? First, consider expanding (7x + 4)(3x + 5) geoff.coates@uwa.edu.au Factorising 20 / 43 Harder Factorisation What if we can’t easily factor out the multiplier of x 2 ? First, consider expanding (7x + 4)(3x + 5) If we do this we get 21x 2 + 35x + 12x + 20 geoff.coates@uwa.edu.au Factorising 20 / 43 Harder Factorisation What if we can’t easily factor out the multiplier of x 2 ? First, consider expanding (7x + 4)(3x + 5) If we do this we get 21x 2 + 35x + 12x + 20 which then equals 21x 2 + 47x + 20 geoff.coates@uwa.edu.au Factorising 20 / 43 Harder Factorisation What if we can’t easily factor out the multiplier of x 2 ? First, consider expanding (7x + 4)(3x + 5) If we do this we get 21x 2 + 35x + 12x + 20 which then equals 21x 2 + 47x + 20 Expansion is easy, but doing this problem backwards is tricky if we don’t know where we started. Our previous methods don’t work here. geoff.coates@uwa.edu.au Factorising 20 / 43 Harder Factorisation In general, when we see an expression of the form Ax 2 + Bx + C we want to factorise it by writing it in the following form: (ax + b)(cx + d) geoff.coates@uwa.edu.au Factorising 21 / 43 Harder Factorisation In general, when we see an expression of the form Ax 2 + Bx + C we want to factorise it by writing it in the following form: (ax + b)(cx + d) Note that a and c multiply to ptoduce the multiplier of x 2 (A), and that b and d multiply to produce the constant on the end (C). geoff.coates@uwa.edu.au Factorising 21 / 43 Harder Factorisation In general, when we see an expression of the form Ax 2 + Bx + C we want to factorise it by writing it in the following form: (ax + b)(cx + d) Note that a and c multiply to ptoduce the multiplier of x 2 (A), and that b and d multiply to produce the constant on the end (C). Then we need to play around with it a bit. geoff.coates@uwa.edu.au Factorising 21 / 43 Harder Factorisation: Example Factorise 2x 2 + 3x + 1. geoff.coates@uwa.edu.au Factorising 22 / 43 Harder Factorisation: Example Factorise 2x 2 + 3x + 1. We need to write this in the form (ax + b)(cx + d). geoff.coates@uwa.edu.au Factorising 22 / 43 Harder Factorisation: Example Factorise 2x 2 + 3x + 1. We need to write this in the form (ax + b)(cx + d). The numbers a and c must multiply up to 2, and so one of them must be 1 and the other must be 2. geoff.coates@uwa.edu.au Factorising 22 / 43 Harder Factorisation: Example Factorise 2x 2 + 3x + 1. We need to write this in the form (ax + b)(cx + d). The numbers a and c must multiply up to 2, and so one of them must be 1 and the other must be 2. (It doesn’t matter which is which because multiplication is commutative.) (2x + b)(x + d) geoff.coates@uwa.edu.au Factorising 22 / 43 Harder Factorisation: Example Factorise 2x 2 + 3x + 1. We need to write this in the form (ax + b)(cx + d). The numbers a and c must multiply up to 2, and so one of them must be 1 and the other must be 2. (It doesn’t matter which is which because multiplication is commutative.) (2x + b)(x + d) The numbers b and d must multiply up to 1, and so one of them must be 1 and the other must be 1. (2x + 1)(x + 1) geoff.coates@uwa.edu.au Factorising 22 / 43 Harder Factorisation: Example Factorise 7x 2 + 15x + 2. geoff.coates@uwa.edu.au Factorising 23 / 43 Harder Factorisation: Example Factorise 7x 2 + 15x + 2. We need to write this in the form (ax + b)(cx + d). geoff.coates@uwa.edu.au Factorising 23 / 43 Harder Factorisation: Example Factorise 7x 2 + 15x + 2. We need to write this in the form (ax + b)(cx + d). The numbers a and c must multiply to 7, and so one of them must be 1 and the other must be 7. It doesn’t matter which is which. (7x + b)(x + d) geoff.coates@uwa.edu.au Factorising 23 / 43 Harder Factorisation: Example Factorise 7x 2 + 15x + 2. We need to write this in the form (ax + b)(cx + d). The numbers a and c must multiply to 7, and so one of them must be 1 and the other must be 7. It doesn’t matter which is which. (7x + b)(x + d) The numbers b and d must multiply to 2, so one of them must be 1 and the other must be 2. The question is, which one is which? There are two possibilities: (7x + 2)(x + 1) geoff.coates@uwa.edu.au (7x + 1)(x + 2) Factorising 23 / 43 Harder Factorisation: Example Factorise 7x 2 + 15x + 2. We need to write this in the form (ax + b)(cx + d). The numbers a and c must multiply to 7, and so one of them must be 1 and the other must be 7. It doesn’t matter which is which. (7x + b)(x + d) The numbers b and d must multiply to 2, so one of them must be 1 and the other must be 2. The question is, which one is which? There are two possibilities: (7x + 2)(x + 1) (7x + 1)(x + 2) To decide which one is correct, expand them both: geoff.coates@uwa.edu.au Factorising 23 / 43 Harder Factorisation: Example Factorise 7x 2 + 15x + 2. We need to write this in the form (ax + b)(cx + d). The numbers a and c must multiply to 7, and so one of them must be 1 and the other must be 7. It doesn’t matter which is which. (7x + b)(x + d) The numbers b and d must multiply to 2, so one of them must be 1 and the other must be 2. The question is, which one is which? There are two possibilities: (7x + 2)(x + 1) (7x + 1)(x + 2) To decide which one is correct, expand them both: 7x 2 + 9x + 2 geoff.coates@uwa.edu.au Factorising 23 / 43 Harder Factorisation: Example Factorise 7x 2 + 15x + 2. We need to write this in the form (ax + b)(cx + d). The numbers a and c must multiply to 7, and so one of them must be 1 and the other must be 7. It doesn’t matter which is which. (7x + b)(x + d) The numbers b and d must multiply to 2, so one of them must be 1 and the other must be 2. The question is, which one is which? There are two possibilities: (7x + 2)(x + 1) (7x + 1)(x + 2) To decide which one is correct, expand them both: 7x 2 + 9x + 2 geoff.coates@uwa.edu.au 7x 2 + 15x + 2 Factorising 23 / 43 Harder Factorisation: Example Factorise 7x 2 + 15x + 2. We need to write this in the form (ax + b)(cx + d). The numbers a and c must multiply to 7, and so one of them must be 1 and the other must be 7. It doesn’t matter which is which. (7x + b)(x + d) The numbers b and d must multiply to 2, so one of them must be 1 and the other must be 2. The question is, which one is which? There are two possibilities: (7x + 2)(x + 1) (7x + 1)(x + 2) To decide which one is correct, expand them both: 7x 2 + 9x + 2 geoff.coates@uwa.edu.au 7x 2 + 15x + 2 Factorising 24 / 43 Harder Factorisation: Example Factorise 6x 2 − 11x − 10. geoff.coates@uwa.edu.au Factorising 25 / 43 Harder Factorisation: Example Factorise 6x 2 − 11x − 10. We need to write this in the form (ax + b)(cx + d). geoff.coates@uwa.edu.au Factorising 25 / 43 Harder Factorisation: Example Factorise 6x 2 − 11x − 10. We need to write this in the form (ax + b)(cx + d). The problem now is that both 6 and 10 have multiple possible factorisations! There are in fact 16 potential answers to test. geoff.coates@uwa.edu.au Factorising 25 / 43 Harder Factorisation: Example Factorise 6x 2 − 11x − 10. We need to write this in the form (ax + b)(cx + d). The problem now is that both 6 and 10 have multiple possible factorisations! There are in fact 16 potential answers to test. The best way to navigate through these options is with a combination of educated guessing and trial-and-error. geoff.coates@uwa.edu.au Factorising 25 / 43 Harder Factorisation: Example Factorise 6x 2 − 11x − 10. We need to write this in the form (ax + b)(cx + d). The problem now is that both 6 and 10 have multiple possible factorisations! There are in fact 16 potential answers to test. The best way to navigate through these options is with a combination of educated guessing and trial-and-error. Start by writing out the potential factorisations of 6 and 10 as follows: geoff.coates@uwa.edu.au Factorising 25 / 43 Harder Factorisation: Example Factorise 6x 2 − 11x − 10. We need to write this in the form (ax + b)(cx + d). The problem now is that both 6 and 10 have multiple possible factorisations! There are in fact 16 potential answers to test. The best way to navigate through these options is with a combination of educated guessing and trial-and-error. Start by writing out the potential factorisations of 6 and 10 as follows: 2 1 2 1 3 6 5 10 6= geoff.coates@uwa.edu.au Factorising 25 / 43 Harder Factorisation: Example Factorise 6x 2 − 11x − 10. We need to write this in the form (ax + b)(cx + d). The problem now is that both 6 and 10 have multiple possible factorisations! There are in fact 16 potential answers to test. The best way to navigate through these options is with a combination of educated guessing and trial-and-error. Start by writing out the potential factorisations of 6 and 10 as follows: 2 1 2 1 3 6 5 10 In this case, the number term (−10) is negative so we need to get a pair whose difference is 11. 6= geoff.coates@uwa.edu.au Factorising 25 / 43 Harder Factorisation: Example Factorise 6x 2 − 11x − 10. We need to write this in the form (ax + b)(cx + d). The problem now is that both 6 and 10 have multiple possible factorisations! There are in fact 16 potential answers to test. The best way to navigate through these options is with a combination of educated guessing and trial-and-error. Start by writing out the potential factorisations of 6 and 10 as follows: 2 1 -2 1 3 6 -5 10 In this case, the number term (−10) is negative so we need to get a pair whose difference is 11. 1 × 2 = 2 and 6 × 5 = 30. Difference 6= 11. Try again. geoff.coates@uwa.edu.au Factorising 25 / 43 Harder Factorisation: Example Factorise 6x 2 − 11x − 10. We need to write this in the form (ax + b)(cx + d). The problem now is that both 6 and 10 have multiple possible factorisations! There are in fact 16 potential answers to test. The best way to navigate through these options is with a combination of educated guessing and trial-and-error. Start by writing out the potential factorisations of 6 and 10 as follows: 2 3 1H *2 HH HH j H 6 5 1 10 In this case, the number term (−10) is negative so we need to get a pair whose difference is 11. 1 × 5 = 5 and 6 × 2 = 12. Difference 6= 11. Try again. geoff.coates@uwa.edu.au Factorising 25 / 43 Harder Factorisation: Example Factorise 6x 2 − 11x − 10. We need to write this in the form (ax + b)(cx + d). The problem now is that both 6 and 10 have multiple possible factorisations! There are in fact 16 potential answers to test. The best way to navigate through these options is with a combination of educated guessing and trial-and-error. Start by writing out the potential factorisations of 6 and 10 as follows: 2 1 -2 1 3 6 -5 10 In this case, the number term (−10) is negative so we need to get a pair whose difference is 11. 2 × 2 = 4 and 3 × 5 = 15. Difference = 11. We have a winner! geoff.coates@uwa.edu.au Factorising 25 / 43 Harder Factorisation: Example Factorise 6x 2 − 11x − 10. We need to write this in the form (ax + b)(cx + d). We have found that 2 × 2 = 4 and 3 × 5 = 15. geoff.coates@uwa.edu.au Factorising 26 / 43 Harder Factorisation: Example Factorise 6x 2 − 11x − 10. We need to write this in the form (ax + b)(cx + d). We have found that 2 × 2 = 4 and 3 × 5 = 15. (2x geoff.coates@uwa.edu.au 5)(3x Factorising 2) 26 / 43 Harder Factorisation: Example Factorise 6x 2 − 11x − 10. We need to write this in the form (ax + b)(cx + d). We have found that 2 × 2 = 4 and 3 × 5 = 15. (2x 5)(3x 2) All we need to do now is place the “+” and “−” signs in the appropriate brackets. geoff.coates@uwa.edu.au Factorising 26 / 43 Harder Factorisation: Example Factorise 6x 2 − 11x − 10. We need to write this in the form (ax + b)(cx + d). We have found that 2 × 2 = 4 and 3 × 5 = 15. (2x − 5)(3x + 2) All we need to do now is place the “+” and “−” signs in the appropriate brackets. geoff.coates@uwa.edu.au Factorising 26 / 43 Harder Factorisation: Example Factorise 6x 2 − 11x − 10. We need to write this in the form (ax + b)(cx + d). We have found that 2 × 2 = 4 and 3 × 5 = 15. (2x − 5)(3x + 2) All we need to do now is place the “+” and “−” signs in the appropriate brackets. So our answer is 6x 2 − 11x − 10 = (2x − 5)(3x + 2). geoff.coates@uwa.edu.au Factorising 26 / 43 A final note on double bracket factorisations Note: Not all expressions of the form ax 2 + bx + c can be factorised into two brackets easily. geoff.coates@uwa.edu.au Factorising 27 / 43 A final note on double bracket factorisations Note: Not all expressions of the form ax 2 + bx + c can be factorised into two brackets easily. Some can’t be facorised at all. For example x 2 + 2x + 2 looks easy but cannot be factorised. geoff.coates@uwa.edu.au Factorising 27 / 43 Why is factorising useful? Factorising is handy for simplifying expressions and equations, which makes formulas more efficient to use and problems easier to solve. geoff.coates@uwa.edu.au Factorising 28 / 43 Why is factorising useful? Factorising is handy for simplifying expressions and equations, which makes formulas more efficient to use and problems easier to solve. Solve for x: x 2 = 6x. geoff.coates@uwa.edu.au Factorising 28 / 43 Why is factorising useful? Factorising is handy for simplifying expressions and equations, which makes formulas more efficient to use and problems easier to solve. Solve for x: x 2 = 6x. x 2 − 6x geoff.coates@uwa.edu.au = 0 (get x terms together) Factorising 28 / 43 Why is factorising useful? Factorising is handy for simplifying expressions and equations, which makes formulas more efficient to use and problems easier to solve. Solve for x: x 2 = 6x. geoff.coates@uwa.edu.au x 2 − 6x = 0 (get x terms together) x(x − 6) = 0 (factorise) Factorising 28 / 43 Why is factorising useful? Factorising is handy for simplifying expressions and equations, which makes formulas more efficient to use and problems easier to solve. Solve for x: x 2 = 6x. x 2 − 6x = 0 (get x terms together) x(x − 6) = 0 (factorise) We know that 0 × a = 0, whatever a is, so only one of the two factors above needs to be 0 to solve the equation: geoff.coates@uwa.edu.au Factorising 28 / 43 Why is factorising useful? Factorising is handy for simplifying expressions and equations, which makes formulas more efficient to use and problems easier to solve. Solve for x: x 2 = 6x. x 2 − 6x = 0 (get x terms together) x(x − 6) = 0 (factorise) We know that 0 × a = 0, whatever a is, so only one of the two factors above needs to be 0 to solve the equation: Either geoff.coates@uwa.edu.au x =0 or Factorising x − 6 = 0. 28 / 43 Why is factorising useful? Factorising is handy for simplifying expressions and equations, which makes formulas more efficient to use and problems easier to solve. Solve for x: x 2 = 6x. x 2 − 6x = 0 (get x terms together) x(x − 6) = 0 (factorise) We know that 0 × a = 0, whatever a is, so only one of the two factors above needs to be 0 to solve the equation: Either x =0 or x − 6 = 0. Hence, the solutions are x = 0 or 6. geoff.coates@uwa.edu.au Factorising 28 / 43 Why is factorising useful? Factorising can also simplify algebraic fractions: geoff.coates@uwa.edu.au Factorising 29 / 43 Why is factorising useful? Factorising can also simplify algebraic fractions: 4x + 6 2 geoff.coates@uwa.edu.au = Factorising 29 / 43 Why is factorising useful? Factorising can also simplify algebraic fractions: 4x + 6 2 geoff.coates@uwa.edu.au = 2(2x + 3) 2 (factorise) Factorising 29 / 43 Why is factorising useful? Factorising can also simplify algebraic fractions: 4x + 6 2 = 2(2x + 3) 2 1 = geoff.coates@uwa.edu.au (factorise) 2(2x + 3) 21 (cancel common factors) Factorising 29 / 43 Why is factorising useful? Factorising can also simplify algebraic fractions: 4x + 6 2 = 2(2x + 3) 2 1 = = geoff.coates@uwa.edu.au (factorise) 2(2x + 3) 21 (cancel common factors) 2x + 3 Factorising 29 / 43 Why is factorising useful? Factorising can also simplify algebraic fractions: geoff.coates@uwa.edu.au Factorising 30 / 43 Why is factorising useful? Factorising can also simplify algebraic fractions: x 2 + 3x + 2 x +1 geoff.coates@uwa.edu.au = Factorising 30 / 43 Why is factorising useful? Factorising can also simplify algebraic fractions: x 2 + 3x + 2 x +1 geoff.coates@uwa.edu.au = (x + 1)(x + 2) x +1 Factorising (factorise) 30 / 43 Why is factorising useful? Factorising can also simplify algebraic fractions: x 2 + 3x + 2 x +1 = (x + 1)(x + 2) x +1 (factorise) 1 = geoff.coates@uwa.edu.au (x + 1)(x + 2) x+ 11 Factorising (cancel common factors) 30 / 43 Why is factorising useful? Factorising can also simplify algebraic fractions: x 2 + 3x + 2 x +1 = (x + 1)(x + 2) x +1 (factorise) 1 = (x + 1)(x + 2) x+ 11 (cancel common factors) = x +2 geoff.coates@uwa.edu.au Factorising 30 / 43 Why is factorising useful? Factorising can also simplify algebraic fractions: x 2 + 3x + 2 x +1 = (x + 1)(x + 2) x +1 (factorise) 1 = (x + 1)(x + 2) x+ 11 (cancel common factors) = x +2 Note: Watch out when you cancel terms involving variables. The original fraction makes it clear that there is a problem when x = −1 because the fraction becomes 0 0 , which is an indeterminate quantity. This problem is no longer obvious in the simplified version. Usually, we would write the answer as x + 2, geoff.coates@uwa.edu.au x 6= −1 Factorising 30 / 43 Polynomials This final section is about polynomials, a topic which may not be on your maths syllabus. geoff.coates@uwa.edu.au Factorising 31 / 43 Polynomials geoff.coates@uwa.edu.au Factorising 32 / 43 Polynomials A polynomial is a bunch of terms involving whole number powers (ie. positive integers) of a variable added/subtracted together. geoff.coates@uwa.edu.au Factorising 32 / 43 Polynomials A polynomial is a bunch of terms involving whole number powers (ie. positive integers) of a variable added/subtracted together. We might also have a constant term (a single number) as well. geoff.coates@uwa.edu.au Factorising 32 / 43 Polynomials A polynomial is a bunch of terms involving whole number powers (ie. positive integers) of a variable added/subtracted together. We might also have a constant term (a single number) as well. 3x 2 − 6x + 7x 5 + 2 geoff.coates@uwa.edu.au Factorising 32 / 43 Polynomials A polynomial is a bunch of terms involving whole number powers (ie. positive integers) of a variable added/subtracted together. We might also have a constant term (a single number) as well. 3x 2 − 6x + 7x 5 + 2 Look at the above polynomial. Every term in it is either a positive integer power of the variable x or a constant term. geoff.coates@uwa.edu.au Factorising 32 / 43 Polynomials A polynomial is a bunch of terms involving whole number powers (ie. positive integers) of a variable added/subtracted together. We might also have a constant term (a single number) as well. 3x 2 − 6x + 7x 5 + 2 Look at the above polynomial. Every term in it is either a positive integer power of the variable x or a constant term. Term 3x geoff.coates@uwa.edu.au Power of x 2 Factorising 32 / 43 Polynomials A polynomial is a bunch of terms involving whole number powers (ie. positive integers) of a variable added/subtracted together. We might also have a constant term (a single number) as well. 3x 2 − 6x + 7x 5 + 2 Look at the above polynomial. Every term in it is either a positive integer power of the variable x or a constant term. Term 3x geoff.coates@uwa.edu.au Power of x 2 2 Factorising 32 / 43 Polynomials A polynomial is a bunch of terms involving whole number powers (ie. positive integers) of a variable added/subtracted together. We might also have a constant term (a single number) as well. 3x 2 − 6x + 7x 5 + 2 Look at the above polynomial. Every term in it is either a positive integer power of the variable x or a constant term. Term Power of x 2 2 3x 7x 5 geoff.coates@uwa.edu.au Factorising 32 / 43 Polynomials A polynomial is a bunch of terms involving whole number powers (ie. positive integers) of a variable added/subtracted together. We might also have a constant term (a single number) as well. 3x 2 − 6x + 7x 5 + 2 Look at the above polynomial. Every term in it is either a positive integer power of the variable x or a constant term. Term Power of x 2 2 5 3x 7x 5 geoff.coates@uwa.edu.au Factorising 32 / 43 Polynomials A polynomial is a bunch of terms involving whole number powers (ie. positive integers) of a variable added/subtracted together. We might also have a constant term (a single number) as well. 3x 2 − 6x + 7x 5 + 2 Look at the above polynomial. Every term in it is either a positive integer power of the variable x or a constant term. Term Power of x 2 2 5 3x 7x 5 −6x geoff.coates@uwa.edu.au Factorising 32 / 43 Polynomials A polynomial is a bunch of terms involving whole number powers (ie. positive integers) of a variable added/subtracted together. We might also have a constant term (a single number) as well. 3x 2 − 6x + 7x 5 + 2 Look at the above polynomial. Every term in it is either a positive integer power of the variable x or a constant term. Term Power of x 2 2 5 1 3x 7x 5 −6x geoff.coates@uwa.edu.au Factorising 32 / 43 Polynomials A polynomial is a bunch of terms involving whole number powers (ie. positive integers) of a variable added/subtracted together. We might also have a constant term (a single number) as well. 3x 2 − 6x + 7x 5 + 2 Look at the above polynomial. Every term in it is either a positive integer power of the variable x or a constant term. Term Power of x 2 2 5 1 3x 7x 5 −6x 2 geoff.coates@uwa.edu.au Factorising 32 / 43 Polynomials A polynomial is a bunch of terms involving whole number powers (ie. positive integers) of a variable added/subtracted together. We might also have a constant term (a single number) as well. 3x 2 − 6x + 7x 5 + 2 Look at the above polynomial. Every term in it is either a positive integer power of the variable x or a constant term. Term 2 3x 7x 5 −6x 2 geoff.coates@uwa.edu.au Power of x 2 5 1 constant term Factorising 32 / 43 Polynomials A polynomial is a bunch of terms involving whole number powers (ie. positive integers) of a variable added/subtracted together. We might also have a constant term (a single number) as well. 3x 2 − 6x + 7x 5 + 2 Look at the above polynomial. Every term in it is either a positive integer power of the variable x or a constant term. Term 2 3x 7x 5 −6x 2 geoff.coates@uwa.edu.au Power of x 2 5 1 constant term or “2x 0 ” Factorising 32 / 43 Polynomials A polynomial is a bunch of terms involving whole number powers (ie. positive integers) of a variable added/subtracted together. We might also have a constant term (a single number) as well. 3x 2 − 6x + 7x 5 + 2 Look at the above polynomial. Every term in it is either a positive integer power of the variable x or a constant term. Term 2 3x 7x 5 −6x 2 geoff.coates@uwa.edu.au Power of x 2 5 1 constant term or “2x 0 ” (so the power of x is 0) Factorising 32 / 43 Polynomials: Examples 7p 8 − 62p 2 + 5 − p 3 geoff.coates@uwa.edu.au Factorising 33 / 43 Polynomials: Examples 7p 8 − 62p 2 + 5 − p 3 7y 2 − 3y 4 geoff.coates@uwa.edu.au Factorising 33 / 43 Polynomials: Examples 7p 8 − 62p 2 + 5 − p 3 7y 2 − 3y 4 3+x geoff.coates@uwa.edu.au Factorising 33 / 43 Polynomials: Examples 7p 8 − 62p 2 + 5 − p 3 7y 2 − 3y 4 3+x 2 5 3q + q 4 + 3q 7 − 2q + 1 (Note that the numbers multiplying the variable parts do not have to be whole numbers.) geoff.coates@uwa.edu.au Factorising 33 / 43 Polynomials: A Convention Polynomials are usually written with their powers in descending order. 7p 8 − 62p 2 + 5 − p 3 geoff.coates@uwa.edu.au Factorising 34 / 43 Polynomials: A Convention Polynomials are usually written with their powers in descending order. 7p 8 − 62p 2 + 5 − p 3 −→ 7p 8 − p 3 − 62p 2 + 5 geoff.coates@uwa.edu.au Factorising 34 / 43 Polynomials: A Convention Polynomials are usually written with their powers in descending order. 7p 8 − 62p 2 + 5 − p 3 −→ 7p 8 − p 3 − 62p 2 + 5 7y 2 − 3y 4 geoff.coates@uwa.edu.au Factorising 34 / 43 Polynomials: A Convention Polynomials are usually written with their powers in descending order. 7p 8 − 62p 2 + 5 − p 3 −→ 7p 8 − p 3 − 62p 2 + 5 7y 2 − 3y 4 −→ −3y 4 + 7y 2 geoff.coates@uwa.edu.au Factorising 34 / 43 Polynomials: A Convention Polynomials are usually written with their powers in descending order. 7p 8 − 62p 2 + 5 − p 3 −→ 7p 8 − p 3 − 62p 2 + 5 7y 2 − 3y 4 −→ −3y 4 + 7y 2 3+x geoff.coates@uwa.edu.au Factorising 34 / 43 Polynomials: A Convention Polynomials are usually written with their powers in descending order. 7p 8 − 62p 2 + 5 − p 3 −→ 7p 8 − p 3 − 62p 2 + 5 7y 2 − 3y 4 −→ −3y 4 + 7y 2 3 + x −→ x + 3 geoff.coates@uwa.edu.au Factorising 34 / 43 Polynomials: A Convention Polynomials are usually written with their powers in descending order. 7p 8 − 62p 2 + 5 − p 3 −→ 7p 8 − p 3 − 62p 2 + 5 7y 2 − 3y 4 −→ −3y 4 + 7y 2 3 + x −→ x + 3 2 5 3q + q 4 + 3q 7 − 2q + 1 geoff.coates@uwa.edu.au Factorising 34 / 43 Polynomials: A Convention Polynomials are usually written with their powers in descending order. 7p 8 − 62p 2 + 5 − p 3 −→ 7p 8 − p 3 − 62p 2 + 5 7y 2 − 3y 4 −→ −3y 4 + 7y 2 3 + x −→ x + 3 2 5 3q + q 4 + 3q 7 − 2q + 1 −→ 3q 7 + 32 q 5 + q 4 − 2q + 1 geoff.coates@uwa.edu.au Factorising 34 / 43 Polynomials: Terminology Consider the following polynomial. 3x 7 − 4x 5 + 37 x 4 − 2x + 9 geoff.coates@uwa.edu.au Factorising 35 / 43 Polynomials: Terminology Consider the following polynomial. 3x 7 − 4x 5 + 37 x 4 − 2x + 9 We say it is a “polynomial in the variable x”. geoff.coates@uwa.edu.au Factorising 35 / 43 Polynomials: Terminology Consider the following polynomial. 3x 7 − 4x 5 + 37 x 4 − 2x + 9 We say it is a “polynomial in the variable x”. The order of a polynomial is the highest power of x present. In this case, the order is geoff.coates@uwa.edu.au Factorising 35 / 43 Polynomials: Terminology Consider the following polynomial. 3x 7 − 4x 5 + 37 x 4 − 2x + 9 We say it is a “polynomial in the variable x”. The order of a polynomial is the highest power of x present. In this case, the order is 7. geoff.coates@uwa.edu.au Factorising 35 / 43 Polynomials: Terminology Consider the following polynomial. 3x 7 − 4x 5 + 37 x 4 − 2x + 9 We say it is a “polynomial in the variable x”. The order of a polynomial is the highest power of x present. In this case, the order is 7. The coefficient of x 7 is 3. (The number multiplying the x part.) geoff.coates@uwa.edu.au Factorising 35 / 43 Polynomials: Terminology Consider the following polynomial. 3x 7 − 4x 5 + 37 x 4 − 2x + 9 We say it is a “polynomial in the variable x”. The order of a polynomial is the highest power of x present. In this case, the order is 7. The coefficient of x 7 is 3. (The number multiplying the x part.) The coefficient of x 5 is geoff.coates@uwa.edu.au Factorising 35 / 43 Polynomials: Terminology Consider the following polynomial. 3x 7 − 4x 5 + 37 x 4 − 2x + 9 We say it is a “polynomial in the variable x”. The order of a polynomial is the highest power of x present. In this case, the order is 7. The coefficient of x 7 is 3. (The number multiplying the x part.) The coefficient of x 5 is −4. geoff.coates@uwa.edu.au Factorising 35 / 43 Polynomials: Terminology Consider the following polynomial. 3x 7 − 4x 5 + 37 x 4 − 2x + 9 We say it is a “polynomial in the variable x”. The order of a polynomial is the highest power of x present. In this case, the order is 7. The coefficient of x 7 is 3. (The number multiplying the x part.) The coefficient of x 5 is −4. The coefficient of x 4 is geoff.coates@uwa.edu.au Factorising 35 / 43 Polynomials: Terminology Consider the following polynomial. 3x 7 − 4x 5 + 37 x 4 − 2x + 9 We say it is a “polynomial in the variable x”. The order of a polynomial is the highest power of x present. In this case, the order is 7. The coefficient of x 7 is 3. (The number multiplying the x part.) The coefficient of x 5 is −4. The coefficient of x 4 is 37 . geoff.coates@uwa.edu.au Factorising 35 / 43 Polynomials: Terminology Consider the following polynomial. 3x 7 − 4x 5 + 37 x 4 − 2x + 9 We say it is a “polynomial in the variable x”. The order of a polynomial is the highest power of x present. In this case, the order is 7. The coefficient of x 7 is 3. (The number multiplying the x part.) The coefficient of x 5 is −4. The coefficient of x 4 is 37 . The coefficient of x is geoff.coates@uwa.edu.au Factorising 35 / 43 Polynomials: Terminology Consider the following polynomial. 3x 7 − 4x 5 + 37 x 4 − 2x + 9 We say it is a “polynomial in the variable x”. The order of a polynomial is the highest power of x present. In this case, the order is 7. The coefficient of x 7 is 3. (The number multiplying the x part.) The coefficient of x 5 is −4. The coefficient of x 4 is 37 . The coefficient of x is −2. geoff.coates@uwa.edu.au Factorising 35 / 43 Polynomials: Terminology Consider the following polynomial. 3x 7 − 4x 5 + 37 x 4 − 2x + 9 We say it is a “polynomial in the variable x”. The order of a polynomial is the highest power of x present. In this case, the order is 7. The coefficient of x 7 is 3. (The number multiplying the x part.) The coefficient of x 5 is −4. The coefficient of x 4 is 37 . The coefficient of x is −2. The coefficient of x 0 is geoff.coates@uwa.edu.au Factorising 35 / 43 Polynomials: Terminology Consider the following polynomial. 3x 7 − 4x 5 + 37 x 4 − 2x + 9 We say it is a “polynomial in the variable x”. The order of a polynomial is the highest power of x present. In this case, the order is 7. The coefficient of x 7 is 3. (The number multiplying the x part.) The coefficient of x 5 is −4. The coefficient of x 4 is 37 . The coefficient of x is −2. The coefficient of x 0 is 9 (constant term). geoff.coates@uwa.edu.au Factorising 35 / 43 Polynomials: Terminology Consider the following polynomial. 3x 7 − 4x 5 + 37 x 4 − 2x + 9 We say it is a “polynomial in the variable x”. The order of a polynomial is the highest power of x present. In this case, the order is 7. The coefficient of x 7 is 3. (The number multiplying the x part.) The coefficient of x 5 is −4. The coefficient of x 4 is 37 . The coefficient of x is −2. The coefficient of x 0 is 9 (constant term). The coefficient of x 2 is geoff.coates@uwa.edu.au Factorising 35 / 43 Polynomials: Terminology Consider the following polynomial. 3x 7 − 4x 5 + 37 x 4 − 2x + 9 We say it is a “polynomial in the variable x”. The order of a polynomial is the highest power of x present. In this case, the order is 7. The coefficient of x 7 is 3. (The number multiplying the x part.) The coefficient of x 5 is −4. The coefficient of x 4 is 37 . The coefficient of x is −2. The coefficient of x 0 is 9 (constant term). The coefficient of x 2 is 0 (because it isn’t there!). geoff.coates@uwa.edu.au Factorising 35 / 43 Polynomials: Terminology Consider the following polynomial. 4x 3 − 5x − 9 What is the order of this polynomial? geoff.coates@uwa.edu.au Factorising 36 / 43 Polynomials: Terminology Consider the following polynomial. 4x 3 − 5x − 9 What is the order of this polynomial? 3 geoff.coates@uwa.edu.au Factorising 36 / 43 Polynomials: Terminology Consider the following polynomial. 4x 3 − 5x − 9 What is the order of this polynomial? 3 What is the coefficient of x 3 ? geoff.coates@uwa.edu.au Factorising 36 / 43 Polynomials: Terminology Consider the following polynomial. 4x 3 − 5x − 9 What is the order of this polynomial? 3 What is the coefficient of x 3 ? 4 geoff.coates@uwa.edu.au Factorising 36 / 43 Polynomials: Terminology Consider the following polynomial. 4x 3 − 5x − 9 What is the order of this polynomial? 3 What is the coefficient of x 3 ? 4 What is the coefficient of x 2 ? geoff.coates@uwa.edu.au Factorising 36 / 43 Polynomials: Terminology Consider the following polynomial. 4x 3 − 5x − 9 What is the order of this polynomial? 3 What is the coefficient of x 3 ? 4 What is the coefficient of x 2 ? 0 geoff.coates@uwa.edu.au Factorising 36 / 43 Polynomials: Terminology Consider the following polynomial. 4x 3 − 5x − 9 What is the order of this polynomial? 3 What is the coefficient of x 3 ? 4 What is the coefficient of x 2 ? 0 What is the coefficient of x? geoff.coates@uwa.edu.au Factorising 36 / 43 Polynomials: Terminology Consider the following polynomial. 4x 3 − 5x − 9 What is the order of this polynomial? 3 What is the coefficient of x 3 ? 4 What is the coefficient of x 2 ? 0 What is the coefficient of x? −5 geoff.coates@uwa.edu.au Factorising 36 / 43 Polynomials: Terminology Consider the following polynomial. 4x 3 − 5x − 9 What is the order of this polynomial? 3 What is the coefficient of x 3 ? 4 What is the coefficient of x 2 ? 0 What is the coefficient of x? −5 What is the coeficient of x 0 ? geoff.coates@uwa.edu.au Factorising 36 / 43 Polynomials: Terminology Consider the following polynomial. 4x 3 − 5x − 9 What is the order of this polynomial? 3 What is the coefficient of x 3 ? 4 What is the coefficient of x 2 ? 0 What is the coefficient of x? −5 What is the coeficient of x 0 ? −9 geoff.coates@uwa.edu.au Factorising 36 / 43 Importance Why are polynomial expressions important? geoff.coates@uwa.edu.au Factorising 37 / 43 Importance Why are polynomial expressions important? They are easier to work with than other expressions (hard to know this unless you have worked with other expressions). geoff.coates@uwa.edu.au Factorising 37 / 43 Importance Why are polynomial expressions important? They are easier to work with than other expressions (hard to know this unless you have worked with other expressions). Most other expressions can be very closely approximated by polynomial expressions. geoff.coates@uwa.edu.au Factorising 37 / 43 Importance Why are polynomial expressions important? They are easier to work with than other expressions (hard to know this unless you have worked with other expressions). Most other expressions can be very closely approximated by polynomial expressions. In a sense, polynomial expressions are mathematical “building blocks”. geoff.coates@uwa.edu.au Factorising 37 / 43 Adding and Subtracting Polynomials When we add or subtract polynomials we get a new polynomial (just like we do with numbers!). This can be done by adding and subtracting their like terms. (4x 2 + 3x + 7) + (2x 2 + 5x + 2) geoff.coates@uwa.edu.au Factorising 38 / 43 Adding and Subtracting Polynomials When we add or subtract polynomials we get a new polynomial (just like we do with numbers!). This can be done by adding and subtracting their like terms. (4x 2 + 3x + 7) + (2x 2 + 5x + 2) We may drop the brackets in this case (why?). 4x 2 + 3x + 7 + 2x 2 + 5x + 2 geoff.coates@uwa.edu.au Factorising 38 / 43 Adding and Subtracting Polynomials When we add or subtract polynomials we get a new polynomial (just like we do with numbers!). This can be done by adding and subtracting their like terms. (4x 2 + 3x + 7) + (2x 2 + 5x + 2) We may drop the brackets in this case (why?). 4x 2 + 3x + 7 + 2x 2 + 5x + 2 If you need to, shift the signed terms around so that like terms are next to each other. 4x 2 + 2x 2 + 3x + 5x + 7 + 2 geoff.coates@uwa.edu.au Factorising 38 / 43 Adding and Subtracting Polynomials When we add or subtract polynomials we get a new polynomial (just like we do with numbers!). This can be done by adding and subtracting their like terms. (4x 2 + 3x + 7) + (2x 2 + 5x + 2) We may drop the brackets in this case (why?). 4x 2 + 3x + 7 + 2x 2 + 5x + 2 If you need to, shift the signed terms around so that like terms are next to each other. 4x 2 + 2x 2 + 3x + 5x + 7 + 2 We now add like terms together. 6x 2 + 8x + 9 geoff.coates@uwa.edu.au Factorising 38 / 43 Adding and Subtracting Polynomials Simplify the following: (3x − 4x 2 + 5) − (x 3 + 3x − 4) 3 geoff.coates@uwa.edu.au Factorising 39 / 43 Adding and Subtracting Polynomials Simplify the following: (3x − 4x 2 + 5) − (x 3 + 3x − 4) 3 There is a negative sign to the left of the second set of brackets. This is effectively a multiplier of −1. From the previous workshop, we know that this −1 gets distributed to each term in the bracket. 3x 3 − 4x 2 + 5 − (x 3 + 3x − 4) geoff.coates@uwa.edu.au Factorising 39 / 43 Adding and Subtracting Polynomials Simplify the following: (3x − 4x 2 + 5) − (x 3 + 3x − 4) 3 There is a negative sign to the left of the second set of brackets. This is effectively a multiplier of −1. From the previous workshop, we know that this −1 gets distributed to each term in the bracket. 3x 3 − 4x 2 + 5 − (x 3 + 3x − 4) = 3x 3 − 4x 2 + 5 geoff.coates@uwa.edu.au Factorising 39 / 43 Adding and Subtracting Polynomials Simplify the following: (3x − 4x 2 + 5) − (x 3 + 3x − 4) 3 There is a negative sign to the left of the second set of brackets. This is effectively a multiplier of −1. From the previous workshop, we know that this −1 gets distributed to each term in the bracket. 3x 3 − 4x 2 + 5 − (x 3 + 3x − 4) = 3x 3 − 4x 2 + 5 geoff.coates@uwa.edu.au Factorising 39 / 43 Adding and Subtracting Polynomials Simplify the following: (3x − 4x 2 + 5) − (x 3 + 3x − 4) 3 There is a negative sign to the left of the second set of brackets. This is effectively a multiplier of −1. From the previous workshop, we know that this −1 gets distributed to each term in the bracket. 3x 3 − 4x 2 + 5 − (x 3 + 3x − 4) = 3x 3 − 4x 2 + 5 − x 3 geoff.coates@uwa.edu.au Factorising 39 / 43 Adding and Subtracting Polynomials Simplify the following: (3x − 4x 2 + 5) − (x 3 + 3x − 4) 3 There is a negative sign to the left of the second set of brackets. This is effectively a multiplier of −1. From the previous workshop, we know that this −1 gets distributed to each term in the bracket. 3x 3 − 4x 2 + 5 − (x 3 + 3x − 4) = 3x 3 − 4x 2 + 5 − x 3 geoff.coates@uwa.edu.au Factorising 39 / 43 Adding and Subtracting Polynomials Simplify the following: (3x − 4x 2 + 5) − (x 3 + 3x − 4) 3 There is a negative sign to the left of the second set of brackets. This is effectively a multiplier of −1. From the previous workshop, we know that this −1 gets distributed to each term in the bracket. 3x 3 − 4x 2 + 5 − (x 3 + 3x − 4) = 3x 3 − 4x 2 + 5 − x 3 − 3x geoff.coates@uwa.edu.au Factorising 39 / 43 Adding and Subtracting Polynomials Simplify the following: (3x − 4x 2 + 5) − (x 3 + 3x − 4) 3 There is a negative sign to the left of the second set of brackets. This is effectively a multiplier of −1. From the previous workshop, we know that this −1 gets distributed to each term in the bracket. 3x 3 − 4x 2 + 5 − (x 3 + 3x − 4) = 3x 3 − 4x 2 + 5 − x 3 − 3x geoff.coates@uwa.edu.au Factorising 39 / 43 Adding and Subtracting Polynomials Simplify the following: (3x − 4x 2 + 5) − (x 3 + 3x − 4) 3 There is a negative sign to the left of the second set of brackets. This is effectively a multiplier of −1. From the previous workshop, we know that this −1 gets distributed to each term in the bracket. 3x 3 − 4x 2 + 5 − (x 3 + 3x − 4) = 3x 3 − 4x 2 + 5 − x 3 − 3x + 4 geoff.coates@uwa.edu.au Factorising 39 / 43 Adding and Subtracting Polynomials Simplify the following: (3x − 4x 2 + 5) − (x 3 + 3x − 4) 3 There is a negative sign to the left of the second set of brackets. This is effectively a multiplier of −1. From the previous workshop, we know that this −1 gets distributed to each term in the bracket. 3x 3 − 4x 2 + 5 − (x 3 + 3x − 4) = 3x 3 − 4x 2 + 5 − x 3 − 3x + 4 (In short, every sign in the 2nd bracket changes.) geoff.coates@uwa.edu.au Factorising 39 / 43 Adding and Subtracting Polynomials Simplify the following: (3x − 4x 2 + 5) − (x 3 + 3x − 4) 3 There is a negative sign to the left of the second set of brackets. This is effectively a multiplier of −1. From the previous workshop, we know that this −1 gets distributed to each term in the bracket. 3x 3 − 4x 2 + 5 − (x 3 + 3x − 4) = 3x 3 − 4x 2 + 5 − x 3 − 3x + 4 (In short, every sign in the 2nd bracket changes.) If you need to, shift the signed terms around so that like terms are next to each other. geoff.coates@uwa.edu.au Factorising 39 / 43 Adding and Subtracting Polynomials Simplify the following: (3x − 4x 2 + 5) − (x 3 + 3x − 4) 3 There is a negative sign to the left of the second set of brackets. This is effectively a multiplier of −1. From the previous workshop, we know that this −1 gets distributed to each term in the bracket. 3x 3 − 4x 2 + 5 − (x 3 + 3x − 4) = 3x 3 − 4x 2 + 5 − x 3 − 3x + 4 (In short, every sign in the 2nd bracket changes.) If you need to, shift the signed terms around so that like terms are next to each other. 3 3 3x − x − 4x 2 − 3x + 5 + 4 geoff.coates@uwa.edu.au Factorising 39 / 43 Adding and Subtracting Polynomials Simplify the following: (3x − 4x 2 + 5) − (x 3 + 3x − 4) 3 There is a negative sign to the left of the second set of brackets. This is effectively a multiplier of −1. From the previous workshop, we know that this −1 gets distributed to each term in the bracket. 3x 3 − 4x 2 + 5 − (x 3 + 3x − 4) = 3x 3 − 4x 2 + 5 − x 3 − 3x + 4 (In short, every sign in the 2nd bracket changes.) If you need to, shift the signed terms around so that like terms are next to each other. 3 3 3x − x − 4x 2 − 3x + 5 + 4 We now add like terms together. geoff.coates@uwa.edu.au Factorising 39 / 43 Adding and Subtracting Polynomials Simplify the following: (3x − 4x 2 + 5) − (x 3 + 3x − 4) 3 There is a negative sign to the left of the second set of brackets. This is effectively a multiplier of −1. From the previous workshop, we know that this −1 gets distributed to each term in the bracket. 3x 3 − 4x 2 + 5 − (x 3 + 3x − 4) = 3x 3 − 4x 2 + 5 − x 3 − 3x + 4 (In short, every sign in the 2nd bracket changes.) If you need to, shift the signed terms around so that like terms are next to each other. 3 3 3x − x − 4x 2 − 3x + 5 + 4 We now add like terms together. 2x 3 − 4x 2 − 3x + 9 geoff.coates@uwa.edu.au Factorising 39 / 43 Adding and Subtracting Polynomials Simplify the following: 4 −2(6x − 7x 2 − 3) + 5(−8x 6 + 3x 4 − 4) geoff.coates@uwa.edu.au Factorising 40 / 43 Adding and Subtracting Polynomials Simplify the following: 4 −2(6x − 7x 2 − 3) + 5(−8x 6 + 3x 4 − 4) Once again, the number out the front of each brackets gets distributed to each of the terms. −2(6x 4 − 7x 2 − 3) + 5(−8x 6 + 3x 4 − 4) geoff.coates@uwa.edu.au Factorising 40 / 43 Adding and Subtracting Polynomials Simplify the following: 4 −2(6x − 7x 2 − 3) + 5(−8x 6 + 3x 4 − 4) Once again, the number out the front of each brackets gets distributed to each of the terms. −2(6x 4 − 7x 2 − 3) + 5(−8x 6 + 3x 4 − 4) = −12x 4 geoff.coates@uwa.edu.au Factorising 40 / 43 Adding and Subtracting Polynomials Simplify the following: 4 −2(6x − 7x 2 − 3) + 5(−8x 6 + 3x 4 − 4) Once again, the number out the front of each brackets gets distributed to each of the terms. −2(6x 4 − 7x 2 − 3) + 5(−8x 6 + 3x 4 − 4) = −12x 4 + 14x 2 geoff.coates@uwa.edu.au Factorising 40 / 43 Adding and Subtracting Polynomials Simplify the following: 4 −2(6x − 7x 2 − 3) + 5(−8x 6 + 3x 4 − 4) Once again, the number out the front of each brackets gets distributed to each of the terms. −2(6x 4 − 7x 2 − 3) + 5(−8x 6 + 3x 4 − 4) = −12x 4 + 14x 2 + 6 geoff.coates@uwa.edu.au Factorising 40 / 43 Adding and Subtracting Polynomials Simplify the following: 4 −2(6x − 7x 2 − 3) + 5(−8x 6 + 3x 4 − 4) Once again, the number out the front of each brackets gets distributed to each of the terms. −2(6x 4 − 7x 2 − 3) + 5(−8x 6 + 3x 4 − 4) = −12x 4 + 14x 2 + 6 − 40x 6 geoff.coates@uwa.edu.au Factorising 40 / 43 Adding and Subtracting Polynomials Simplify the following: 4 −2(6x − 7x 2 − 3) + 5(−8x 6 + 3x 4 − 4) Once again, the number out the front of each brackets gets distributed to each of the terms. −2(6x 4 − 7x 2 − 3) + 5(−8x 6 + 3x 4 − 4) = −12x 4 + 14x 2 + 6 − 40x 6 + 15x 4 geoff.coates@uwa.edu.au Factorising 40 / 43 Adding and Subtracting Polynomials Simplify the following: 4 −2(6x − 7x 2 − 3) + 5(−8x 6 + 3x 4 − 4) Once again, the number out the front of each brackets gets distributed to each of the terms. −2(6x 4 − 7x 2 − 3) + 5(−8x 6 + 3x 4 − 4) = −12x 4 + 14x 2 + 6 − 40x 6 + 15x 4 − 20 geoff.coates@uwa.edu.au Factorising 40 / 43 Adding and Subtracting Polynomials Simplify the following: 4 −2(6x − 7x 2 − 3) + 5(−8x 6 + 3x 4 − 4) Once again, the number out the front of each brackets gets distributed to each of the terms. −2(6x 4 − 7x 2 − 3) + 5(−8x 6 + 3x 4 − 4) = −12x 4 + 14x 2 + 6 − 40x 6 + 15x 4 − 20 If you need to, shift the signed terms around so that like terms are next to each other. −12x 4 + 15x 4 + 14x 2 + 6 − 20 − 40x 6 geoff.coates@uwa.edu.au Factorising 40 / 43 Adding and Subtracting Polynomials Simplify the following: 4 −2(6x − 7x 2 − 3) + 5(−8x 6 + 3x 4 − 4) Once again, the number out the front of each brackets gets distributed to each of the terms. −2(6x 4 − 7x 2 − 3) + 5(−8x 6 + 3x 4 − 4) = −12x 4 + 14x 2 + 6 − 40x 6 + 15x 4 − 20 If you need to, shift the signed terms around so that like terms are next to each other. −12x 4 + 15x 4 + 14x 2 + 6 − 20 − 40x 6 We now add like terms together and write with decreasing powers: −40x 6 + 3x 4 + 14x 2 − 14 geoff.coates@uwa.edu.au Factorising 40 / 43 Multiplying Polynomials We can use the distributive law to multiply two polynomials together (3x 2 + 2x)(4x 5 + 3x) = geoff.coates@uwa.edu.au Factorising 41 / 43 Multiplying Polynomials We can use the distributive law to multiply two polynomials together (3x 2 + 2x)(4x 5 + 3x) = geoff.coates@uwa.edu.au Factorising 41 / 43 Multiplying Polynomials We can use the distributive law to multiply two polynomials together (3x 2 + 2x)(4x 5 + 3x) = 12x 7 geoff.coates@uwa.edu.au Factorising 41 / 43 Multiplying Polynomials We can use the distributive law to multiply two polynomials together (3x 2 + 2x)(4x 5 + 3x) = 12x 7 geoff.coates@uwa.edu.au Factorising 41 / 43 Multiplying Polynomials We can use the distributive law to multiply two polynomials together (3x 2 + 2x)(4x 5 + 3x) = 12x 7 + 9x 3 geoff.coates@uwa.edu.au Factorising 41 / 43 Multiplying Polynomials We can use the distributive law to multiply two polynomials together (3x 2 + 2x)(4x 5 + 3x) = 12x 7 + 9x 3 geoff.coates@uwa.edu.au Factorising 41 / 43 Multiplying Polynomials We can use the distributive law to multiply two polynomials together (3x 2 + 2x)(4x 5 + 3x) = 12x 7 + 9x 3+ 8x 6 geoff.coates@uwa.edu.au Factorising 41 / 43 Multiplying Polynomials We can use the distributive law to multiply two polynomials together (3x 2 + 2x)(4x 5 + 3x) = 12x 7 + 9x 3+ 8x 6 geoff.coates@uwa.edu.au Factorising 41 / 43 Multiplying Polynomials We can use the distributive law to multiply two polynomials together (3x 2 + 2x)(4x 5 + 3x) = 12x 7 + 9x 3+ 8x 6+ 6x 2 geoff.coates@uwa.edu.au Factorising 41 / 43 Multiplying Polynomials We can use the distributive law to multiply two polynomials together (3x 2 + 2x)(4x 5 + 3x) = 12x 7 + 9x 3+ 8x 6+ 6x 2 Every term in the first bracket meets every term in the second bracket. (We saw this in the previous workshop.) geoff.coates@uwa.edu.au Factorising 41 / 43 Multiplying Polynomials We can use the distributive law to multiply two polynomials together (3x 2 + 2x)(4x 5 + 3x) = 12x 7 + 9x 3+ 8x 6+ 6x 2 Every term in the first bracket meets every term in the second bracket. (We saw this in the previous workshop.) Sometimes, we work with “longer” polynomials. The rule is still the same. Every term in the first bracket must meet every term in the second bracket. geoff.coates@uwa.edu.au Factorising 41 / 43 Expansion In general (polynomial) × (polynomial) geoff.coates@uwa.edu.au Factorising 42 / 43 Expansion In general (polynomial) × (polynomial) expands out to polynomial geoff.coates@uwa.edu.au Factorising 42 / 43 Expansion In general (polynomial) × (polynomial) expands out to polynomial Note: We saw earlier that 2nd order polynomials can (sometimes) be factorised. geoff.coates@uwa.edu.au Factorising 42 / 43 Expansion In general (polynomial) × (polynomial) expands out to polynomial Note: We saw earlier that 2nd order polynomials can (sometimes) be factorised. In general, polynomials can also (sometimes) be be factorised. geoff.coates@uwa.edu.au Factorising 42 / 43 Expansion In general (polynomial) × (polynomial) expands out to polynomial Note: We saw earlier that 2nd order polynomials can (sometimes) be factorised. In general, polynomials can also (sometimes) be be factorised. However, that’s a topic for another time . . . geoff.coates@uwa.edu.au Factorising 42 / 43 Using STUDYSmarter Resources This resource was developed for UWA students by the STUDYSmarter team for the numeracy program. When using our resources, please retain them in their original form with both the STUDYSmarter heading and the UWA crest. geoff.coates@uwa.edu.au Factorising 43 / 43