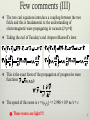Download Maxwell equations

PHY 042: Electricity and Magnetism
Maxwell’s equations
Prof. Hugo Beauchemin
1
Limitation of Ampere’s law
 With Faraday’s law, we extended the electrostatics E-field to non-
steady current, providing a set of equations for E-fields valid in any
classical situations and describing all possible experiments
 However, there is still an opened question:
Is Ampere’s law still valid when currents are non-steady?
 No, as is, Ampere’s law is limited to statics situations
Static case!
 Maxwell spotted this limitation and proposed an extension:
Use continuity equation to add a term guaranteeing that the
divergence of the curl of B is always null for any current
2
The displacement current
 The extra term added by Maxwell to yield divergenceless curl for the
B-field in non-static situation changed Ampere’s law:
A changing electric field induces a magnetic field!
 Maxwell’s term was named displacement current:
It restores charge conservation in Ampere’s law for non-static case
 All magnetostatics results obtained are preserved
 Brought a complete symmetry between the E-field and the B-field
 Hard to observe, so not in disagreement with previous experiments, but
can be tested once it is expected/predicted

 Purely theoretical addition, making new predictions for
experiments in non-static situation!
3
The typical example
 Consider a circuit with a charging up capacitor
 Assume plates are large compared to their separation
 Use infinite capacitor plate approximation

Assume weak steady current
 No induced EMF and uniform static charge distribution on plates

These small assumptions need to be carefully controlled in a real
experiment to allow for a measurement of the wanted effects
 By Biot-Savart, the B-field due to current in iii) and iv) is:
 B must be continuous at the boundary of region iii) and ii)

No plate with surface current
between regions ii) and iii)
iii)
 No wire can yield a B-field in ii)
 Ampere’s law on JD must be added
to satisfy boundary conditions
ii)
i)
iv)
4
Maxwell equations
 We have a set of differential equations completely determining:
How charges produce an E-field and a B-field
 How a varying E-field or B-field generates the other field
 How the fields affect the motion of charges

Differential form
Integral form
i)
ii)
iii)
iv)
v)
5
Few comments (I)
1. The continuity equation, expressing the charge conservation, is a
consequence of iv) and can be obtained from the divergence of iv)
2. To solve actual problems (make predictions for experiments), we
need to know the boundary conditions

Boundary conditions are exactly the same as those found in electroand magneto-statics:
3. If we are dealing with materials, it is convenient to write Maxwell’s
equations in terms of free charges and currents

Note that if the E-field varies in time, so will the polarization, thus
generating a flow of bound charges
6
Few comments (II)

Maxwell’s equations are written in terms of B, H, D, E and must thus
be supplemented with constitutive equations
and

Typically only given in terms of E and H
 Control potentials and currents
4. The large symmetry between E and B is understood in special
relativity as the fact that E and B are related by Lorentz transform.

This complete the unification of E and B
For a boost
along x-axis
7
Few comments (III)
 The two curl equations introduce a coupling between the two
fields and this is fundamental to the understanding of
electromagnetic wave propagating in vacuum (J=r=0)
 Taking the curl of Faraday’s and Ampere-Maxwell’s laws:
 This is the exact form of the propagation of progressive wave
functions
 The speed of this wave is v = (m0e0)-1 = 2.998 × 108 m/s = c
 These waves are light!!!!
8