Download Prove Triangles Similar by AA,SSS and SAS

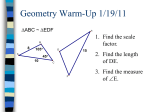
6.4, 6.5
Name:________________
Prove Triangles Similar by AA, SSS and SAS
Learning Target: By the end of today’s lesson we will be able to successfully use the AA, SSS or SAS
Similarity Postulates.
Angle-Angle (AA) Similarity Postulate:
If two angles of one triangle are congruent to two angles
of another triangle, then the two triangles are similar.
JKL ~ XYZ
Example 1: Determine whether the triangles are similar. If they are, write a similarity statement.
Explain your reasoning.
a.)
b.)
c.)
Example 2: Show that the two triangles are similar.
a.)
RTV and RQS
b.)
LMN and NOP
Side-Side-Side (SSS) Similarity Theorem:
If the corresponding side lengths of two triangles are proportional
then the triangles are similar.
If
AB BC CA
=
=
, then ∆ABC ~ ∆RST.
RS ST TR
c.)
BCD and EFD
Example 3: Is either ∆DEF or ∆GHJ similar to ∆ABC?
Example 4: Find the value of x that makes ∆ABC ~ ∆DEF.
Side-Angle-Side (SAS) Similarity Theorem:
If an angle of one triangle is congruent to an angle of a second triangle and
the lengths of the sides including these angles are ______________, then
the triangles are similar.
If ∠X ≅ ∠M , and
ZX
XY
=
, then ∆XYZ ∼ ∆MNP.
PM MN
Example 5: A lifeguard is standing beside the lifeguard chair on a beach. The lifeguard is 6 feet 4 inches tall
and casts a shadow that is 48 inches long. The chair casts a shadow that is 6 feet long. Are the
triangles similar. If so, how tall is the chair?
***************************************************************************************************************************************
Triangle Similarity Postulate and Theorems:
AA Similarity Postulate:
SSS Similarity Theorem:
If ∠A ≅ ∠D and ∠B ≅ ∠E, then ∆ABC ~ ∆DEF.
(If 2 angles of 1 triangle = 2 angles of another triangle they are similar)
If
AB BC AC
=
=
, then ∆ABC ~ ∆DEF.
DE EF DF
(If all sides of 1 triangle proportional to all sides of another triangle they are similar)
SAS Similarity Theorem: If ∠A ≅ ∠D and
AB AC
=
, then ∆ABC ∼ ∆DEF.
DE DF
(If all 2sides of 1 triangle proportional to 2 sides of another triangle and the included angles are =
then the triangles are similar)