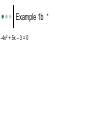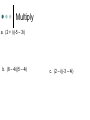Download 5.6 – Quadratic Equations and Complex Numbers

5.6 – Quadratic
Equations and
Complex Numbers
Objectives:
Classify and find all roots of a quadratic equation.
Graph and perform operations on complex numbers.
Standard:
2.5.11.C. Present mathematical procedures and results
clearly, systematically, succinctly and correctly.
The Solutions to a Quadratic Equation can
referred to as ANY of the following:
x – intercepts
Solutions
Roots
Zeroes
Discriminant
The expression b2– 4ac is called the discriminant
of a quadratic equation.
 If b2– 4ac > 0 (positive), the formula will give two
real number solutions.
 If b2– 4ac = 0, there will be one real number
solution, called a double root.
 If b2– 4ac < 0 (negative), the formula gives no real
solutions

Ex 1. Find the discriminant for each
equation. Then determine the number of
real solutions for each equation by using
the discriminant.
Imaginary Numbers
i  1
If r > 0, then the imaginary number  r is defined as
follows:
 r   1 r   1  r  i r
Example 1a
Example 1b *
-4x2 + 5x – 3 = 0
Example 1c *
6x2 – 3x + 1 = 0
Complex Numbers
Example 1a and b*
b. 2x + 3iy = -8 + 10i
Operations with Complex
Numbers
c. (-10 – 6i) + (8 – i)
Multiply
a. (2 + i)(-5 – 3i)
b. (6 – 4i)(5 – 4i)
c. (2 – i)(-3 – 4i)
Conjugate of a Complex
Number
 The
conjugate of a complex number
a + bi is a – bi.
 To simplify a quotient with an imaginary
number in the denominator, multiply by a
fraction equal to 1, using the conjugate of
the denominator.
 This process is called rationalizing the
denominator.
4+3i
5 - 4i
-7+ 6i
-9 - i
Example 1a
2  5i
Rationalize the fraction:
2  3i
2  5i 2  3i

Next step : FOIL
2  3i 2  3i
(2)( 2)  (2)(3i)  (5i)( 2)  (5i )(3i)
(2)( 2)  (2)(3i)  (3i)( 2)  (3i)(3i)
4  6i  10i  15i 2
2
4  6i  6i  9i
4  16i  15
49
 11  16i
13
11 16
  i
13 13
Example 1b
3  4i
Rationalize the fraction:
2i
Writing Questions
Homework
Pg. 320 #14-86 even