Download ee221_8

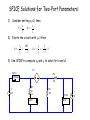
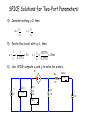
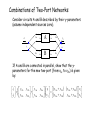
Circuits II
EE221
Unit 8
Instructor: Kevin D. Donohue
2 Port Networks –Impedance/Admittance,
Transmission, and Hybird Parameters
2-Port Circuits


Network parameters characterize linear circuits that have
both input and output terminals, in terms of linear equations
that describe the voltage and current relationships at those
terminals. This model provides critical information for
understanding the effects of connecting circuits, loads, and
sources together at the input and output terminals of a twoport circuit. A similar model was used when dealing with oneport circuits.
Review example: Thévenin and Norton Equivalent Circuits:
100 
10 i1
a
i1
10 V
50 
100 
b
Show that Voc=8 V, Isc = 0.08 A, and Rth = 100
2-Port Circuits:
Now take away the source from the previous example:
100 
10 ia
ia
50 



100 
Why wouldn't it make sense to talk about a Thévenin or
Norton equivalent circuit in this case?
The Thévenin and Norton models must be extended to
describe circuit behavior at two ports.
Label the terminal voltage and currents as v1, i1, v2, and i2
and develop a mathematical relationship to show their
dependencies.
Inverse Transmission -Parameter Model:
If the circuit is linear, then a general linear relationship between
the terminal voltages and currents can be expressed as:
v2  av1  bi1  V2
i2  cv1  di1  I 2


Geometrically each equation forms a planar surface over the v1-i1
plane, therefore, only three non-colinear points on the surface
are necessary to uniquely determine a, b, c, d, V2, and I2. So if
the circuit response is known for three different values of the
v1-i1 pairs, six equations with six unknowns can be generated and
solved.
This problem can be simplified by strategically setting v1 and i1 to
zero in order to isolate unknown parameters and simplify the
resulting equations. In general, if no independent sources exist
in the circuit, then V2 and I2 will be 0. This will be the case for
the problems considered in this unit.
Example
Determine the inverse transmission parameter model for the
given circuit.
100 
10 ia
i1
+
v1
-
ia
50 
100 
i2
+
v2
-
Show that a =18/5, b= 100, c = 7/250 Siemens, d= 1.
Summary Formula for Inverse Transmission
Parameters:

If all independent sources are deactivated, set i1 = 0 to find:
a

v2
v1
c
i1  0
i2
v1
i1  0
If all independent sources are deactivated, set v1 = 0 to find:
b
v2
i1
d 
v1  0
i2
i1
v1  0
Equivalent Circuit for Inverse Transmission
Parameter Model:
If inverse transmission parameters are known, then the
following circuit can be used as an equivalent circuit:
i1
+
-
+
v1
-
i2
1
i2
c
+
-
d
c
+
-
av1
 bi1
+
v2
-
This circuit is helpful when implementing in SPICE without
knowledge or details of circuit from which parameters
were derived.
SPICE Solutions for Two-Port Parameters:
By strategically selecting the constraints on port variables, the
two-port parameters are the ratios of other port variables.
Therefore:



Port variables can be constrained by attaching a zero-valued voltage
or current source. The other port can be excited by a unity-valued
source (or some other convenient value).
Place meters at remaining ports to obtain values for evaluating ratios.
The two-port parameter can be found from values determined
through SPICE.
Example: Determine the SPICE commands to find the abcd
parameters for the circuit below.
100 
10 ia
i1
+
v1
-
ia
50 
100 
i2
+
v2
-
SPICE Solutions for Two-Port Parameters:
1)
Consider setting v1=0, then
v
i
b 2
d  2
i1
i1
2)
Excite the circuit with i2=1 then
b
v2
100

i1
1
d 
i2
1

1
i1
1
3) Use SPICE to compute v2 and i1 to solve for b and d.
VAm1
H1
R2
-1000.00m
100
0
V1
R1
50
VAma
16.67n
R3
100
1
IVm2
100.00
I2
SPICE Solutions for Two-Port Parameters:
4)
Consider setting i1=0, then
v2
a
v1
5)
i2
v1
Excite the circuit with v2=1, then
a
6)
c
1
1

 3.6
v1 0.2778
c
i2 .00778

 28m
v1 0.2778
Use SPICE compute v1 and i2 to solve for a and c.
H1
R2
VAm2
7.78m
100
0
I1
IVm1
277.78m
R1
50
VAma
5.56m
R3
100
1
V2
Transmission -Parameter Model:
Transmission parameters are related to the
inverse transmission parameters by reversing
the independent and dependent variables:
Transmission
Parameters
v2  av1  bi1
i2  cv1  di1
v2  a b   v1 
 i    c d   i 
 1
 2 
Inverse Transmission
Parameters
1
a b  v2   v1 
 c d   i    i 

  2   1
 A B   v2  v1 
C D   i    i 

 2   1 
v1  Av2  Bi 2
i1  Cv2  Di2
Impedance/Admittance-Parameter Model:
Impedance Parameters
v1  z11i1  z12i2
v2  z21i1  z22i2
 v1   z11
v    z
 2   21
z12   i1 
z22  i2 
Admittance Parameters
1
 z11 z12   v1   i1 
 
z



 21 z 22  v2  i2 
 y11 y12   v1   i1 
 
y



 21 y22  v2  i2 
i1  y11v1  y12v2
i2  y21v1  y22v2
Hybrid (h)/Inverse Hybrid (g)-Parameter
Model:
Hybrid Parameters
v1  h11i1  h12v2
i2  h21i1  h22v2
v1   h11 h12   i1 
 i   h



 2   21 h22  v2 
Inverse Hybrid Parameters
1
 h11 h12  v1   i1 
 



h
 21 h22  i2  v2 
 g11 g12  v1   i1 
 



g
 21 g 22   i2  v2 
i1  g11v1  g12i2
v2  g 21v1  g 22i2
Relationship Between 2 Sets of Port Parameters:
Since a single set of network parameters characterize the linear
circuits completely at the input and output terminals, it is
possible to derive other network parameters from this set.
Example: Consider the z and y parameter characterization of a
given circuit with no independent sources:
v   z
 
v   z
1
2
z  i 
 
z  i 
11
12
21
i   y
 
i   y
1
22
2
Show that:
z

 z
11
21
z  y

z   y
12
22
11
21
y 

y 
1
12
1
11
2
21
y

y y  y y

y

 y y  y y
11
21
y  z

y   z
11
12
22
11
21
12
22
1
22
2
22
21
12
21
22
z 

z 
12
22
11
y

 y
y  v 
 
y  v 
1
22
21
12
z

z z  z z

z

 z z  z z
22
11
22
21
12
21
11
22
21
12
y

y y y y 

y

y y  y y 
12
11
22
21
12
21
12
11
11
22
z

z z z z 

z

z z  z z 
12
11
22
21
12
21
12
11
11
22
Relationship Between 2 Sets of Port Parameters:
Example: Consider the abcd and h parameter characterization of
a given circuit with no independent sources:
v   h
 
 i  h
v2  a b   v1 
 i    c d   i 
 1
 2 
1
11
2
21
h  i

h  v
12
1
22
2



Show that:
 h11
h
 21
 b
h12   a

h22   bc  ad
 a
1
a
c

a
 1 

 h11 
 
 

a
b

  h12 
h
 12 

 c d   

  h22    h  h22h11 


 21

h
h
12  

 12 
Terminal Currents and Voltages from Port
Parameters:
Once the port parameters are known, no other information from
the circuit is required to determine the behavior of the
currents and voltages at the terminals.
Example: Given the z-parameter representation of a circuit,
determine the resulting terminal voltages and currents when a
practical source with internal resistance Rs and voltage Vs is
connected to the input (terminal 1) and a load RL is connected to
the output (terminal 2):
v   z
 
v   z
1
11
2
21
z  i 
 
z  i 
12
22
Show that:
z
11
L
z
s
12
RV 
v 
R R  R
21
L
s
1
L
s
z
22
L
R
L

R R
z R 
RV 

R R
L
22
R R
s
R
L
z
L
s
L
22
s
2
L
s
z R
22
s
R
v 
R R  R 
z R
z R 
12
L
L
s
s
+
v2
-
+
v1
-
Vs
2
i2
i1
Rs
1
s
z
22
R
L

 z
11
-
RL
RV 
L
s
z R V 
z R 
21
L
12
R R
L
s
s
s
z R
22
s
Combinations of Two-Port Networks:
Consider circuits A and B described by their abcdparameters (assume independent sources zero).
i1a
-
+
v1a
-
A
+
v2a
-
i2a
i1b
-
-
i2b
+
v1b
-
B
+
v2b
-
-
If A and B are connected in series, show that the abcd
parameters for the new two-port (from v1a to v2b) is given
by:
v2b  ab
 i   c
 2b   b
bb  aa
db   ca
ba   v1a   ab aa  bb ca




d a   i1a  cb aa  db ca
abba  bb d a   v1a 
cbba  db d a   i1a 
Combinations of Two-Port Networks:
Consider circuits A and B described by their y-parameters
(assume independent sources zero).
i1a
i1
+
- v1
+
v1a
-
A
+
v2a
-
-
-
-
i1b
-
i2a
+
v1b
-
B
+
v2b
-
i2b
i2
+
v2-
-
If A and B are connected in parallel, show that the yparameters for the new two-port (from v1a to v2b) is given
by:
 i1    y11b
i     y
 2    21b
y12b   y11a


y22b   y21a
y12a    v1    y11a  y11b 
   

y22a   v2   y21a  y21b 
 y12a  y12b   v1 
y22a  y22b  v2 