![[Part 1]](http://s1.studyres.com/store/data/008795788_1-6323173b144ce5752d9cfa6a3116d3f8-300x300.png)
subclasses of p-valent starlike functions defined by using certain
... In order to complete the proof of Theorem 6.1, we note that the result is sharp for the function ∈ ∗, , , , , of the form ...
... In order to complete the proof of Theorem 6.1, we note that the result is sharp for the function ∈ ∗, , , , , of the form ...
Notes on logic, sets and complex numbers
... 1) Equality between sets: Two sets A and B are equal if and only if they have exactly the same elements. A = B ⇐⇒ for any x ( x ∈ A ↔ x ∈ B). 2) Subsets and Proper subsets: We say that A is a subset of B and we write A ⊆ B or B ⊇ A if every element of A is also an element of B. We say that A is a pr ...
... 1) Equality between sets: Two sets A and B are equal if and only if they have exactly the same elements. A = B ⇐⇒ for any x ( x ∈ A ↔ x ∈ B). 2) Subsets and Proper subsets: We say that A is a subset of B and we write A ⊆ B or B ⊇ A if every element of A is also an element of B. We say that A is a pr ...
MIDTERM REVIEW FOR MATH 500 1. The limit Define limn→∞ an
... In class, we provide several examples and theorems to explain how we use the completeness Axiom establish some surprising properties of the real numbers, for instance, the Archimedean property of real numbers, and the “approximation” of any numbers in R by integers, and approximation of real numbers ...
... In class, we provide several examples and theorems to explain how we use the completeness Axiom establish some surprising properties of the real numbers, for instance, the Archimedean property of real numbers, and the “approximation” of any numbers in R by integers, and approximation of real numbers ...
Formal power series
... In the ring of formal power series, the binomial theorem tell us that if n is any non-negative integer, (1+f)^n is equal to the “infinite sum” 1 + [n ]f + [n(n-1)/2] f^2 + [n(n-1)(n-2)/6] f^3 + ... (which isn’t so infinite, since all but finitely many terms vanish). But in fact this is true for neg ...
... In the ring of formal power series, the binomial theorem tell us that if n is any non-negative integer, (1+f)^n is equal to the “infinite sum” 1 + [n ]f + [n(n-1)/2] f^2 + [n(n-1)(n-2)/6] f^3 + ... (which isn’t so infinite, since all but finitely many terms vanish). But in fact this is true for neg ...
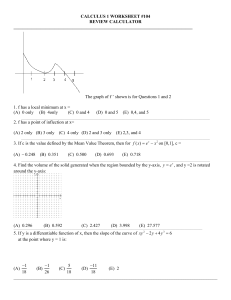
Calculus Questions
... of the questions pertain to topics covered in a typical Calculus I course; the rest pertain to topics covered in a typical Calculus II course. Answer the questions on the electronic grading form by giving the best answer to each question. The scoring will be done by giving one point for each questio ...
... of the questions pertain to topics covered in a typical Calculus I course; the rest pertain to topics covered in a typical Calculus II course. Answer the questions on the electronic grading form by giving the best answer to each question. The scoring will be done by giving one point for each questio ...
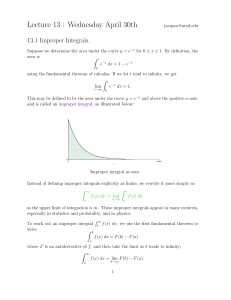
Fundamental theorem of calculus
The fundamental theorem of calculus is a theorem that links the concept of the derivative of a function with the concept of the function's integral.The first part of the theorem, sometimes called the first fundamental theorem of calculus, is that the definite integration of a function is related to its antiderivative, and can be reversed by differentiation. This part of the theorem is also important because it guarantees the existence of antiderivatives for continuous functions.The second part of the theorem, sometimes called the second fundamental theorem of calculus, is that the definite integral of a function can be computed by using any one of its infinitely-many antiderivatives. This part of the theorem has key practical applications because it markedly simplifies the computation of definite integrals.