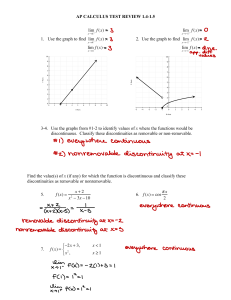
AP CALCULUS TEST REVIEW 1.4-1.5 1. Use the graph to find lim f(x)
... 3-4. Use the graphs from #1-2 to identify values of x where the functions would be discontinuous. Classify these discontinuities as removable or non-removable. ...
... 3-4. Use the graphs from #1-2 to identify values of x where the functions would be discontinuous. Classify these discontinuities as removable or non-removable. ...
An Exponential Function with base b is a function of the form: f(x
... We know the meaning of br if r is a rational number. What if r is irrational? What we do is we approximate the value of br by using rational approximate for r. For example, to approximate 5π , we may approximate it as 53.12 , 53.141 , 53.1415 , 53.14159 .... In advance mathematics one can define the ...
... We know the meaning of br if r is a rational number. What if r is irrational? What we do is we approximate the value of br by using rational approximate for r. For example, to approximate 5π , we may approximate it as 53.12 , 53.141 , 53.1415 , 53.14159 .... In advance mathematics one can define the ...
Math 3, Midterm Exam 1, Question 11
... • Thus, since f (x) = 2x for x 0, we have that f (x) is continuous for x < 0 (note that we don’t have continuity for free at 0). So far, we have shown that f (x) is continuous the set of all real numbers except 0. Now we need to address the continuity at x = 0, for that we recall the definition, f ...
... • Thus, since f (x) = 2x for x 0, we have that f (x) is continuous for x < 0 (note that we don’t have continuity for free at 0). So far, we have shown that f (x) is continuous the set of all real numbers except 0. Now we need to address the continuity at x = 0, for that we recall the definition, f ...
Fundamental theorem of calculus
The fundamental theorem of calculus is a theorem that links the concept of the derivative of a function with the concept of the function's integral.The first part of the theorem, sometimes called the first fundamental theorem of calculus, is that the definite integration of a function is related to its antiderivative, and can be reversed by differentiation. This part of the theorem is also important because it guarantees the existence of antiderivatives for continuous functions.The second part of the theorem, sometimes called the second fundamental theorem of calculus, is that the definite integral of a function can be computed by using any one of its infinitely-many antiderivatives. This part of the theorem has key practical applications because it markedly simplifies the computation of definite integrals.