A note on two linear forms
... deals with three consecutive minimal points xj−1 , xj , xj+1 lying in a two-dimensional linear subspace, say π. We should note that our definition of minimal points differs from those in [2, 3, 11]. However the main argument is the same. It is discussed in our survey [8]. One may look for the approxim ...
... deals with three consecutive minimal points xj−1 , xj , xj+1 lying in a two-dimensional linear subspace, say π. We should note that our definition of minimal points differs from those in [2, 3, 11]. However the main argument is the same. It is discussed in our survey [8]. One may look for the approxim ...
On the rational approximation to the binary Thue–Morse–Mahler
... quotients equal to 4 or 5. Furthermore, there are infinitely many pairs of consecutive partial quotients both less than or equal to 5. n ...
... quotients equal to 4 or 5. Furthermore, there are infinitely many pairs of consecutive partial quotients both less than or equal to 5. n ...
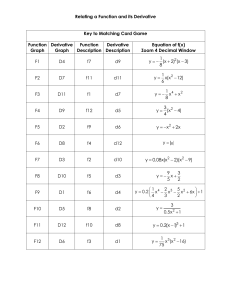
description of derivative
... The graph of this derivative is not positive for all x in [–3, 3], and is symmetric to the y-axis. d1 ...
... The graph of this derivative is not positive for all x in [–3, 3], and is symmetric to the y-axis. d1 ...
FOUNDATIONS OF MARTINGALE THEORY AND
... (Xt )t≥0 and (Yt )t≥0 are called indistinguishable if almost everywhere Xt = Yt for all t ∈ T , i.e. there is a set N such that for all t ∈ T equality Xt (ω) = Yt (ω) holds true for ω ∈ / N . A stochastic process is called cadlag or RCLL (caglad or LCRL) if the sample paths t 7→ Xt (ω) are right con ...
... (Xt )t≥0 and (Yt )t≥0 are called indistinguishable if almost everywhere Xt = Yt for all t ∈ T , i.e. there is a set N such that for all t ∈ T equality Xt (ω) = Yt (ω) holds true for ω ∈ / N . A stochastic process is called cadlag or RCLL (caglad or LCRL) if the sample paths t 7→ Xt (ω) are right con ...
Prove
... To prove a theorem (proposition, lemma) of the form p ⇒ q, we often attempt to build a bridge of implications p ⇒ p1 ⇒ p2 ⇒ · · · ⇒ q2 ⇒ q1 ⇒ q. To obtain such a bridge, we might try to use deductive reasoning (”what can we conclude from p?”) to get p1 from p, then again to get p2 from p1 , and so o ...
... To prove a theorem (proposition, lemma) of the form p ⇒ q, we often attempt to build a bridge of implications p ⇒ p1 ⇒ p2 ⇒ · · · ⇒ q2 ⇒ q1 ⇒ q. To obtain such a bridge, we might try to use deductive reasoning (”what can we conclude from p?”) to get p1 from p, then again to get p2 from p1 , and so o ...
BASIC NOTIONS AND RESULTS IN TOPOLOGY 1. Metric spaces A
... Compact sets are bounded and closed as in Rn , but the converse is far from being true in this generality! Exercise 1. If X is compact then it is complete and separable. Theorem 1.3. A set Y ⊂ X is compact if and only if from every open cover {Uα }α∈A of Y we can extract a finite cover. Proof. The s ...
... Compact sets are bounded and closed as in Rn , but the converse is far from being true in this generality! Exercise 1. If X is compact then it is complete and separable. Theorem 1.3. A set Y ⊂ X is compact if and only if from every open cover {Uα }α∈A of Y we can extract a finite cover. Proof. The s ...
Fundamental theorem of calculus
The fundamental theorem of calculus is a theorem that links the concept of the derivative of a function with the concept of the function's integral.The first part of the theorem, sometimes called the first fundamental theorem of calculus, is that the definite integration of a function is related to its antiderivative, and can be reversed by differentiation. This part of the theorem is also important because it guarantees the existence of antiderivatives for continuous functions.The second part of the theorem, sometimes called the second fundamental theorem of calculus, is that the definite integral of a function can be computed by using any one of its infinitely-many antiderivatives. This part of the theorem has key practical applications because it markedly simplifies the computation of definite integrals.