AP Calculus – Final Review Sheet When you see the words …. This
... Typically done with a table of values. Be sure to use only values that are given. If you are given 6 sets of points, you can only do 3 midpoint rectangles. base x0 2 x1 2 x2 ... 2 xn1 xn A ...
... Typically done with a table of values. Be sure to use only values that are given. If you are given 6 sets of points, you can only do 3 midpoint rectangles. base x0 2 x1 2 x2 ... 2 xn1 xn A ...
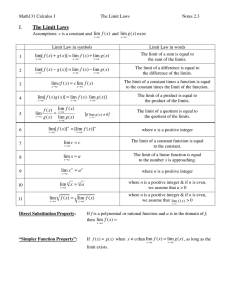
I. The Limit Laws
... If f ( x) ≤ g ( x) when x is near a (except possibly at a) and the limits of f and g both exist as x approaches a then lim f ( x ) ≤ lim g ( x ) . x→a ...
... If f ( x) ≤ g ( x) when x is near a (except possibly at a) and the limits of f and g both exist as x approaches a then lim f ( x ) ≤ lim g ( x ) . x→a ...
Political Space Curves or : The unreasonable resilience of calculations
... Is the sustainability of Vahlen’s arguments unreasonable, or supreme proof of the cumulative character of the development of mathematics ? ...
... Is the sustainability of Vahlen’s arguments unreasonable, or supreme proof of the cumulative character of the development of mathematics ? ...
THE ARITHMETIC LARGE SIEVE WITH AN APPLICATION TO THE
... which up to the po (1) factor is the best known result today. Conjecturally, Ankeny showed that GRH gives an even better estimate than Vinogradov conjectured, showing GRH implies np (log p)2 . We will prove a result of Linnik which shows that Vinogradov’s conjecture holds for all but very few prim ...
... which up to the po (1) factor is the best known result today. Conjecturally, Ankeny showed that GRH gives an even better estimate than Vinogradov conjectured, showing GRH implies np (log p)2 . We will prove a result of Linnik which shows that Vinogradov’s conjecture holds for all but very few prim ...
Fundamental theorem of calculus
The fundamental theorem of calculus is a theorem that links the concept of the derivative of a function with the concept of the function's integral.The first part of the theorem, sometimes called the first fundamental theorem of calculus, is that the definite integration of a function is related to its antiderivative, and can be reversed by differentiation. This part of the theorem is also important because it guarantees the existence of antiderivatives for continuous functions.The second part of the theorem, sometimes called the second fundamental theorem of calculus, is that the definite integral of a function can be computed by using any one of its infinitely-many antiderivatives. This part of the theorem has key practical applications because it markedly simplifies the computation of definite integrals.