Wilson`s Theorem and Fermat`s Theorem
... Example. φ(24) = 8, because there are eight positive integers less than 24 which are relatively prime to 24: ...
... Example. φ(24) = 8, because there are eight positive integers less than 24 which are relatively prime to 24: ...
Lectures on Number Theory
... Definition 1.1 An integer b is divisible by an integer a, written a | b, if there is an integer x such that b = ax. We also say that b is a multiple of a, and that a is a divisor of b. Any integer a has ±1 and ±a as divisors. These divisors are called trivial. The proof of the following simple prope ...
... Definition 1.1 An integer b is divisible by an integer a, written a | b, if there is an integer x such that b = ax. We also say that b is a multiple of a, and that a is a divisor of b. Any integer a has ±1 and ±a as divisors. These divisors are called trivial. The proof of the following simple prope ...
Analysis Notes (only a draft, and the first one!)
... Since, given x, the element y that satisfies A3 is unique, we can name this element as a function of x. We will denote it by −x and call it the additive inverse of x or just “minus x”. Therefore, we have: x + (−x) = (−x) + x = 0. ...
... Since, given x, the element y that satisfies A3 is unique, we can name this element as a function of x. We will denote it by −x and call it the additive inverse of x or just “minus x”. Therefore, we have: x + (−x) = (−x) + x = 0. ...
Synopsis of linear associative algebra. A report on its natural
... 6 SYNOPSIS OF LINEAR ASSOCIATIVE ALGEBRA We find the first such general treatment in Hamilton's theory1 of sets. The first extensive attempt at development of algebras in this way was made by Benjamin Peirce2. His memoir was really epoch-making. It has been critic- ally examined by Hawkes3, who has ...
... 6 SYNOPSIS OF LINEAR ASSOCIATIVE ALGEBRA We find the first such general treatment in Hamilton's theory1 of sets. The first extensive attempt at development of algebras in this way was made by Benjamin Peirce2. His memoir was really epoch-making. It has been critic- ally examined by Hawkes3, who has ...
Fundamental theorem of calculus
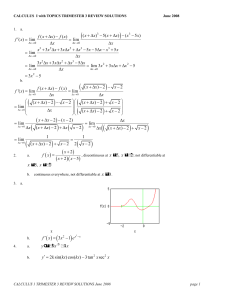
The fundamental theorem of calculus is a theorem that links the concept of the derivative of a function with the concept of the function's integral.The first part of the theorem, sometimes called the first fundamental theorem of calculus, is that the definite integration of a function is related to its antiderivative, and can be reversed by differentiation. This part of the theorem is also important because it guarantees the existence of antiderivatives for continuous functions.The second part of the theorem, sometimes called the second fundamental theorem of calculus, is that the definite integral of a function can be computed by using any one of its infinitely-many antiderivatives. This part of the theorem has key practical applications because it markedly simplifies the computation of definite integrals.