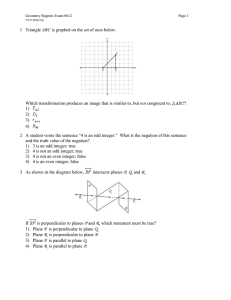
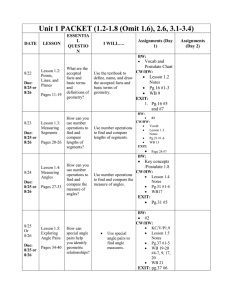
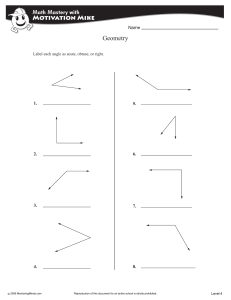
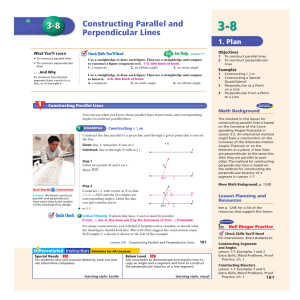
The SMSG Axioms for Euclidean Geometry
... visualized but cannot be defined. Any attempt at a definition ends up circling around the terms and using one to define the other. These are the basic building blocks of the geometry. It is usually a good idea to have a mental image of the undefined terms – a visualization of the objects and how the ...
... visualized but cannot be defined. Any attempt at a definition ends up circling around the terms and using one to define the other. These are the basic building blocks of the geometry. It is usually a good idea to have a mental image of the undefined terms – a visualization of the objects and how the ...
8.2
... 1. If lines l and m in a plane are intersected by a transversal in such a way that alternate interior angles are of equal measure, then l is parallel to m 2. Alternate interior angles formed by two parallel lines and a transversal are of equal measure ...
... 1. If lines l and m in a plane are intersected by a transversal in such a way that alternate interior angles are of equal measure, then l is parallel to m 2. Alternate interior angles formed by two parallel lines and a transversal are of equal measure ...
common core 3.2 gem
... 4. Which is a true statement about the measure of ∠DCJ? A It equals 30°, by the Alternate Interior Angles Theorem. B It equals 30°, by the Corresponding Angles Postulate. C It equals 50°, by the Alternate Interior Angles Theorem. D It equals 50°, by the Corresponding Angles Postulate. 5. Which is a ...
... 4. Which is a true statement about the measure of ∠DCJ? A It equals 30°, by the Alternate Interior Angles Theorem. B It equals 30°, by the Corresponding Angles Postulate. C It equals 50°, by the Alternate Interior Angles Theorem. D It equals 50°, by the Corresponding Angles Postulate. 5. Which is a ...
5.3 Parallel Lines and Congruent Angles
... Consecutive Angles Consecutive Interior Angles: Two angles that lie between parallel lines on the same sides of the transversal. ...
... Consecutive Angles Consecutive Interior Angles: Two angles that lie between parallel lines on the same sides of the transversal. ...
GeometryPowerStandards Student Copy
... ● LT3: Construct a viable argument to justify a solution method. ● LT4: Identify pairs of angles as complementary, supplementary, adjacent, or vertical, and apply these relationships to determine missing angle measures ● LT5: Prove triangles congruent using SSS, SAS, ASA, AAS, and HL. Prove parts of ...
... ● LT3: Construct a viable argument to justify a solution method. ● LT4: Identify pairs of angles as complementary, supplementary, adjacent, or vertical, and apply these relationships to determine missing angle measures ● LT5: Prove triangles congruent using SSS, SAS, ASA, AAS, and HL. Prove parts of ...
GETE0308
... Converse of the Alternate Interior Angles Theorem or on the theorem In a plane, if two lines are perpendicular to the same line, then they are parallel to each other. The method for constructing perpendicular lines is based on the method for constructing the perpendicular bisector of a segment in Le ...
... Converse of the Alternate Interior Angles Theorem or on the theorem In a plane, if two lines are perpendicular to the same line, then they are parallel to each other. The method for constructing perpendicular lines is based on the method for constructing the perpendicular bisector of a segment in Le ...
Perspective (graphical)

Perspective (from Latin: perspicere to see through) in the graphic arts is an approximate representation, on a flat surface (such as paper), of an image as it is seen by the eye. The two most characteristic features of perspective are that objects are smaller as their distance from the observer increases; and that they are subject to foreshortening, meaning that an object's dimensions along the line of sight are shorter than its dimensions across the line of sight.Italian Renaissance painters including Paolo Uccello, Piero della Francesca and Luca Pacoima studied linear perspective, wrote treatises on it, and incorporated it into their artworks, thus contributing to the mathematics of art.